Re: L'infini est-il limité ?

[hks]

le schéma reprend la répartition en 7 phases ( voir les 7 jours de la création dans la bible)
Etonnant non !!!
bon je passe
Le fil ne m'intéresse guère ...en fait.

[neopilina]

Les pythagoriciens ont rencontré et traité ce genre de problème !! Tu as raison de mettre des guillemets à " empilant ". Les pythagoriciens se sont effectivement demandés si un plan résulte d'un tel " empilement ", si un volume résulte d'un tel " empilement " de plans ? Je pense que non, et il me semble que les mathématiques répondent également non.

Les mathématiques répondent oui. La théorie mathématique de l'intégration permet de voir un carré comme un empilement d'une infinité de segments vus comme des rectangles de longueur fixe et de largeur infiniment petite. Selon cette théorie, l'aire de chacun de ces rectangles infinitésimaux vaut bien zéro, mais la "somme" d'une infinité de ces rectangles peut donner une aire résultante qui est supérieure à zéro.

Voilà un message, un type de message, que j'attendais depuis longtemps. Je m'explique. Parce que je ne suis pas en mesure d'en juger par moi-même et parce que j'accorde un certain crédit, un crédit certain !, à ton discours, je suis tout à fait disposé à croire ce que tu me dis : qu'il en est ainsi mathématiquement.
Et pourtant, a contrario, etc., pour moi (mon cerveau, ma façon de fonctionner a priori, etc.), ce que tu dis ci-dessus, je ne peux pas le concevoir : pour moi, " l'empilement " d'objets à une dimension (droite, segment) qui donnerait un objet à deux dimensions (un plan) est impossible, carrément un oxymore. Pour moi, un segment, une droite, ne peuvent que se superposer à un autre, c'est tout. Voilà un exemple où la légendaire rigueur des mathématiques me semble faire défaut à elle-même.

La question de l’infini a donné lieu à de nombreux travaux en mathématiques, notamment à la suite de Cantor.
Mais j’aborderai la question d’une autre façon, qui rejoint votre problématique, en me référant à l’Ethique de Spinoza.
La chose finie y est posée comme une chose bornée par une autre chose et je dirai donc qu’est in-finie une chose non bornée par une autre chose.
D’autre part, ayant défini la substance et l’attribut comme ce que l’intellect perçoit d’une substance comme constituant son essence, Spinoza définit Dieu  comme une substance consistant en une infinité d’attributs.
Une " infinité d’attributs ", cela ne signifie pas un nombre infini d’attributs mais que Dieu, conçu dans son essence, n’est pas borné.
L’homme connaît l’attribut Pensée et l’attribut Etendue de Dieu mais on ne peut pas dire qu’il connaît deux attributs de Dieu.
Un attribut de Dieu et un attribut de Dieu, ça ne fait pas deux attributs de Dieu.
Spinoza démontre qu’à part Dieu, il n’y a pas de substance.
Il n’y a donc qu’une substance : Dieu et cette unicité de la substance est à rapprocher de l’Être des Éléates.

A propos de la dernière proposition :

Il n’y a donc qu’une substance : Dieu et cette unicité de la substance est à rapprocher de l’Être des Éléates.

Non, pour deux raisons :

- Même si la critique éléate conduit à distinguer " être " avec minuscule et " Être " avec majuscule, surtout à cause de Zénon (son propos n'a pas d'autre solution que la version intelligible de l'étant, donc l'Etant généré, formalisé, par un être vivant, au cas échéant, Sujet philosophique, c'est à dire nous), eux-même ne le font pas clairement (" ils ne transforment pas l'essai ", ce que je pense possible aujourd'hui, grâce à l'émancipation de la science), notamment Parménide dans son poème, où il est bien question de l'être au sens philosophique le plus classique qui soit, qui deviendra, afin d'éviter certains écueils survenus avec la critique éléate, substance chez Aristote et Spinoza. Aujourd'hui, grâce au divorce de la science d'avec la philosophie, on sait que les anciennes problématiques de l'être, de la substance, etc., ne relèvent pas, de prime abord en tous cas, de la philosophie, mais bien de la science.

- Parménide est un animiste, un païen : les Dieux aussi c'est de l'être, au sens où il l'entend dans le poème, sous une forme ou une autre, et non l'inverse. Ils font partie du monde, de l'univers (Epicure disait joliment : " Qu'on m'explique Chaos [la première entité nommée dans la Théogonie d'Hésiode], je vous fais grâce de tout le reste ", et force est de constater qu'il a toujours diablement raison). Dans la philosophie occidentale, il faut attendre la dérive, l'inversion, la révolution, coperniciennes, téléologique socratique, platonicienne, et son couronnement aristotélicien, pour que l'Occident deviennent philosophiquement monothéiste, pour qu'ait lieu la dite inversion (et on comprend alors très bien que l'Occident était fin prêt à accueillir, à occidentaliser, via le Nouveau Testament, une prédication juive) : on a un Dieu créateur, voilà pour la physique (le Premier Moteur chez Aristote, la substance de Spinoza, etc.) et Législateur, voilà pour la métaphysique, et voilà nos deux très très gros, les deux plus gros, problèmes ainsi résolus. Une thèse qui reste ultra-dominante, sous une foule de formes, dans le monde entier, ce qui inclut le spinozisme.

Je te rappelle mes positions :
- Pas de vie, pas d'Être, pas d'Etants, avec majuscule.
- Pas de Sujet, pas de Dieu. Ce qui n'amoindrit en rien l'extrême intérêt et l'extrême importance qu'il revêt pour chacun d'entre nous et ce le plus radicalement qui soit. Qu'on utilise ou pas le mot " Dieu ", il semble bien que c'est grâce à ce genre d'événements, d'effractions, etc., que nous progressons à titre historique. A titre personnel, ça ne me dérange absolument pas de dire que les " Lumières " (quand bien même certaines d'entre elles se sont montrées furieusement athées, le Dieu qu'elles rejetaient et dont Nietzsche annonce la mort, je le rejette aussi), c'est un événement " divin ", on repousse les Murs, l'Horizon, les Paradigmes, etc. de façon irrémédiable. Je postule qu'ici, tout ce qui est une fois sorti de cette " Boite " ne peut pas y être remis, malgré les efforts, bien réels, des conservateurs, réactionnaires, de tout poil ! Il faudra faire avec, le seul remède à la connaissance, si elle embarrasse, c'est plus de connaissance. Pour parler le " spinozien ", il faut toujours plus de connaissances du deuxième genre noir sur blanc afin de faciliter plus de connaissances du troisième genre chez le plus grand nombre de Sujets possible.

Plus récemment, j'ai abordé cette hypothèse : celle d'un cogito pour le vivant, la vie, en soi, pour la première, la plus radicale, expression de la Subjectivité, qui serait de percevoir, de sentir, de voir, etc., de l'être, de la substance, partout moi inclus, ce dont on a fait une thèse philosophique. En fait donc, " cogito " pour la vie, c'est toujours déjà de facto, de mon fait, du fait de mon corps, de l'Être, des Etants, biologiquement dit (en tant que mammifère), puis philosophiquement dit (c'est Moi qui écrit présentement, pas Vanleers). Mais ce que voit, constate, la science, c'est le continu, l'espace, le temps, la matière, fondamentalement interdépendants, ce qu'a montré la relativité générale, si on touche un " curseur ", la valeur, de l'un des trois dans une équation, cela se répercute de facto, mécaniquement, sur les deux autres. Mes efforts du moment c'est donc d'examiner les rapports entre le continu de la physique et l'Être, les Etants, que je génère a priori, d'abord physiquement, biologiquement, puisqu'ils constituent ma Relation a priori " forcée ", fonctionnelle, constitutive, au réel, en ayant donc bien conscience (cogito), à l'esprit, que ceux-ci (Être et Etants) sont de Mon fait, en tant qu'être vivant, puis, cogito classique, conscience de Soi, de Mon fait en tant que tel Sujet et pas un Autre.

[Magni]

le schéma reprend la répartition en 7 phases ( voir les 7 jours de la création dans la bible)
Etonnant non !!!
bon je passe
Le fil ne m'intéresse guère ...en fait.

Ton message n'était pas très intéressant non plus, de mon point de vue.

Si tu veux on n'en parle pas.

[Vanleers]

Et pourtant, a contrario, etc., pour moi (mon cerveau, ma façon de fonctionner a priori, etc.), ce que tu [Leonhard] dis ci-dessus, je ne peux pas le concevoir : pour moi, " l'empilement " d'objets à une dimension (droite, segment) qui donnerait un objet à deux dimensions (un plan) est impossible, carrément un oxymore. Pour moi, un segment, une droite, ne peuvent que se superposer à un autre, c'est tout. Voilà un exemple où la légendaire rigueur des mathématiques me semble faire défaut à elle-même.

Je suis d’accord : un empilement de segments de droite ne donne pas un carré.
Je vous ai signalé un lien qui montre clairement et simplement qu’à tout point d’un carré on peut faire correspondre un point d’un côté du carré de façon univoque.
Et réciproquement qu’à tout point d’un côté du carré on peut faire correspondre un point du carré de façon univoque.
Autrement dit, on peut établir une bijection de l’ensemble infini des points du carré sur l’ensemble infini des points du côté.
Ces deux ensembles infinis sont dits équipotents : de façon imagée, on dira qu’il y a autant de points dans le carré que de points sur l’un de ses côtés, « ni plus ni moins ».

Je ne sais pas si l’infini en mathématiques peut être employé de façon féconde en philosophie.
Je réfléchis à ce que vous avez écrit sur les Éléates.

[Magni]

Si un empilement de segments de droite ne donne pas un carré alors un empilement de points ne donne pas une droite.


Le problème se situe déjà au niveau de la ligne. C'est l'hypothèse du continu, qui est synonyme de "non dénombrable".

Est ce que tu acceptes comme naturel (ou pas) qu'un segment de droite peut être un empilement de points les uns à coté des autres de façon que leur succession est continue ?
Une succession de points, entités ponctuelles et sans dimension, réparties sur le segment de droite de façon qu'il n'y a pas d'espace entre chaque point.

Une fois que ça c'est construit mathématiquement, on passe de la ligne au plan avec une succession de lignes juxtaposée de façon continues. Utiliser des rectangles de largueur nulle peu aussi faire l'affaire.

[Magni]

Pour la science, le monde physique est réputé non continu mais on a besoin du continu en mathématique pour calculer de nombreux aspects du monde physique.

Aristote réfutait l'existence de l'infini en acte, tandis qu'il admettait l'infini en puissance.



Prenons un électron autour d'un proton.

Calculons toutes les positions où il pourrait se trouver.
Les position possibles sont infinies, c'est l'infini en puissance.
Mesurons la position de l'électron.
Il n'y aura pas une infinité de mesure, on n'a pas d'infini en acte.

On a besoin du continu en mathématique pour calculer le possible.

Accepter de considérer un segment continu c'est comme dire c'est comme dire que la quantité des possibles est indénombrable.
Cela ne signifie pas que la quantité des positions réelles successive est infinie.

[hks]

Je suis  informé sur la théorie du big bang... disons que je la subis puisque auditeur régulier de l"émission de france culture  "la méthode scientifique".

Pour moi ce n'est pas une théorie scientifique suffisamment fondée, il y a une grande part d'imaginaire là dedans.

je m'intéresse plus à l'imagination qui forme l'image qu'à l'image elle même.
ainsi, évidemment, qu'au fondement philosophiques de la théorie .
Fondements métaphysiques épistémologiques et psychologiques.  

Les physiciens grand public passent souvent là dessus. Ils développent d'emblée la théorie.

Je ne dis pas non plus que les philosophes soient suffisamment armés, il y a un divorce au bénéfice des physiciens et de la dite théorie.


J'ai eu récemment sous les yeux (au moins un texte)
d'un célèbre philosophe américain lequel  défend bec et ongle la théorie du big bang .
William Lane Craighttp://wikimonde.com/article/William_Lane_Craig

Ce philosophe est évangéliste  et défend par ailleurs les preuves de la résurrection du christ.
D 'où ma remarque sur le coté biblique de l'image postée.


https://bibleetsciencediffusion.org/index.php/2020/03/24/creation-et-cosmologie-du-big-bang-par-william-lane-craig/
.......................................

Mon message est tout bête, et je ne crois pas qu'un astrophysicien me démentira : nous n'avons pas la preuve scientifique que l'univers a une origine, et nous n'avons pas la preuve qu'il n'y a pas d'origine. Cessons de prendre le fait que l'univers aurait eu une origine comme une vérité indiscutable.

https://information.tv5monde.com/info/l-univers-ne-commence-pas-avec-le-big-bang-entretien-avec-etienne-klein-3847

[Leonhard]

Et pourtant, a contrario, etc., pour moi (mon cerveau, ma façon de fonctionner a priori, etc.), ce que tu [Leonhard] dis ci-dessus, je ne peux pas le concevoir : pour moi, " l'empilement " d'objets à une dimension (droite, segment) qui donnerait un objet à deux dimensions (un plan) est impossible, carrément un oxymore. Pour moi, un segment, une droite, ne peuvent que se superposer à un autre, c'est tout. Voilà un exemple où la légendaire rigueur des mathématiques me semble faire défaut à elle-même.

Un empilement d'un nombre fini de segments ne donne pas un carré. Mais un empilement d'un nombre infini de rectangles de hauteurs infiniment petites, ça peut.

L'idée est de considérer un empilement d'un nombre fini de N rectangles de hauteur 1/N, et d'imaginer ce que cela devient quand N augmente :



En poussant le processus jusqu'à l'infini, on se retrouve avec une infinité de rectangles de hauteurs infiniment petites, qui constituent bel et bien le même carré.

[jean tardieu]

Si un photon voyage pendant 13.4 milliards d’années et parcourt 45 milliards d’années-lumière à cause de l’expansion universelle

Ce qui impliquerait que le photon aille plus vite que lui-même...
Pourquoi pas, dans certaines conditions...
Cela impliquerait-il, d'une façon ou d'une autre, le phénomène d'intrication ...?

[Leonhard]

L'expansion de l'univers n'est pas un phénomène dans lequel les objets de l'univers s'éloigneraient, dans l'espace, les uns des autres.

C'est plutôt un phénomène où l'espace lui-même, conçu comme une substance "élastique", se dilate.

Une image classique est celle d'un ballon de baudruche avec des fourmis qui se déplacent dessus. Pour les fourmis, la vitesse maximale possible par rapport au sol est celle de la lumière. Mais le ballon lui-même se dilate, avec pour effet que deux fourmis peuvent sembler s'éloigner à une vitesse supérieure à celle de la lumière.

[jean tardieu]

L'expansion de l'univers n'est pas un phénomène dans lequel les objets de l'univers s'éloigneraient, dans l'espace

Pourtant les galaxies s'éloignent les unes des autres...
Je ne mets pas en doute le modèle standard, il est extrêmement fiable puisqu'il est extrêmement prédictif. Ce sont sans doute les observations qui sont en cause.
Il faut aussi compter avec les "autoroutes" gravitationnelles.

[Magni]

Quand on observe le fond diffus cosmologique, ce qu'on voit ce sont les photons qui touchent le récepteur, on ne voit pas a distance, on ne voit que les photons qui arrivent jusqu'à nous.

Un photon qui est parti il y a 13.4 milliard d'années à parcouru 13.4 milliards d'années lumières dans l'espace (il n'a pas "parcouru" 45 comme j'ai écris abusivement).

La distance qui nous sépare aujourd'hui de la surface de dernière diffusion est d'environ 43 milliards d'années-lumière, soit plus de trois fois la distance qu'a parcouru la lumière du fond diffus cosmologique entre son époque d'émission et maintenant. Elle était de seulement 40 millions d'années-lumière à l'époque où le rayonnement a été émis.

Le fait que les photons du fond diffus cosmologique ait mis 13,4 milliards d'années pour parcourir une distance qui était initialement de 40 millions d'années-lumière vient du fait qu'à l'époque de son émission, quand ils avançaient d'un kilomètre, la région dans laquelle nous nous trouvons s'était éloignée de bien plus d'un kilomètre du fait de l'expansion de l'Univers (qui était donc plus rapide que la vitesse de la lumière), un peu à l'image d'un marcheur qui prendrait un tapis roulant à contre-sens et qui marcherait moins vite que le tapis. Ce n'est que quand l'expansion de l'Univers ralentit suffisamment (en dessous de la vitesse de la lumière) que les photons purent finalement se rapprocher de leur point de destination. Avant cela, bien qu'ils se dirigeaient vers celui-ci, ils s'en éloignaient constamment.


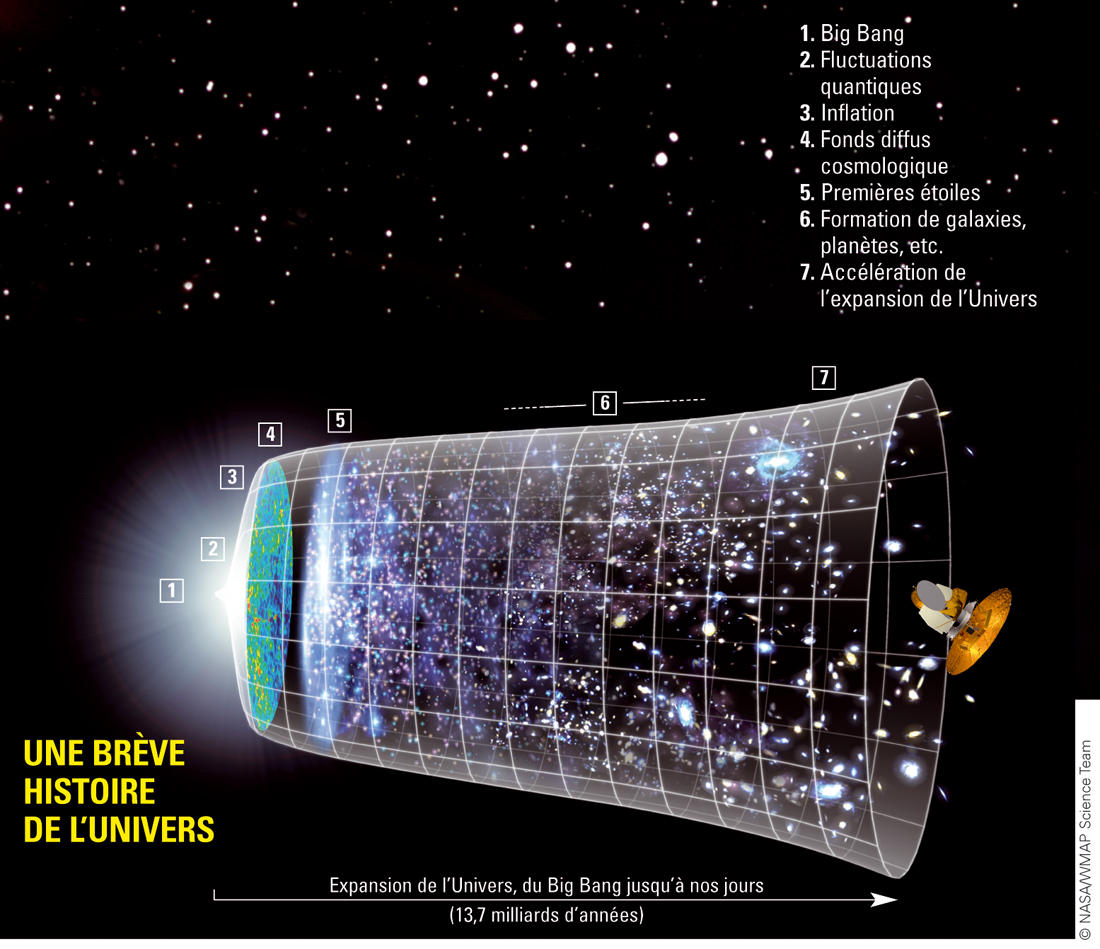
Et donc cette illustration (from the Wilkinson Microwave Anisotropy Probe Science Team of NASA) est bien plus artistique que scientifique, on a l'impression que la taille de l'univers ne s'est étendue que de 10% entre le moment du premier rayonnement et maintenant (entre les points 4 et 7) mais le rayon cosmologique est passé de 40 million à 43 milliard d'années lumière, soit une augmentation de cent dix mille pour cent.
Il ne faut retenir la dedans que l'ordre des étapes.

On peut aussi faire abstraction des points blancs dans la partie haute de l'image qui représentent d'autres univers et qui sont totalement artistico-hypothétiques et n'ont rien de scientifique.

A droite en jaune, le satellite PROBE, celui-ci est tout à fait réel.

[jean tardieu]

Précisons que depuis cet article de wiki surface de dernière diffusion, des ondes gravitationnelles ont bien été captées, et il s'en enregistre de plus en plus ....Originaires de supernovae ...??? de coalescence de trous noirs...???

[Vanleers]

L'idée est de considérer un empilement d'un nombre fini de N rectangles de hauteur 1/N, et d'imaginer ce que cela devient quand N augmente :



En poussant le processus jusqu'à l'infini, on se retrouve avec une infinité de rectangles de hauteurs infiniment petites, qui constituent bel et bien le même carré.

Remarquons que tous ces rectangles (ces « tiroirs ») contiennent la même « quantité infinie » Q de points et leur réunion aussi.
Si bien qu’on a NxQ = Q
Cette équation a 0 pour solution évidente : si tous les tiroirs sont vides, leur réunion est vide également.
Mais il y a une autre solution, paradoxale : ∞ car :
N x ∞ = ∞
Si tous les tiroirs sont bourrés d’une quantité infinie de points, leur réunion aussi mais sans qu’il y en ait plus dans leur réunion que dans n’importe lequel d’entre eux, aussi petit soit-il.
Mieux encore, si le tiroir est réduit à l’état de non-tiroir, d’une hauteur nulle , il est encore plein de la même quantité infinie Q de points.
C’est le paradis des commerçants de points : ils peuvent vendre tous les points qu’ils veulent et même une infinité, leur stock ne bouge pas.

[jean tardieu]

Certes mais n'oublie pas qu'il existe aussi un infini allant de 1 à 2, puis de 2 à 3, et ainsi de suite dans les ensembles D. Le stock est alors insignifiant comme objets de commerce.

[Leonhard]

Remarquons que tous ces rectangles (ces « tiroirs ») contiennent la même « quantité infinie » Q de points et leur réunion aussi.
Si bien qu’on a NxQ = Q
Cette équation a 0 pour solution évidente : si tous les tiroirs sont vides, leur réunion est vide également.
Mais il y a une autre solution, paradoxale : ∞ car :
N x ∞ = ∞

Vous êtes nombreux à avoir fait des calculs avec l'infini. Mais il faut savoir que d'un point de vue algébrique, l'ajout des infinis exige de renoncer à des propriétés algébriques classiques, avec pour conséquence que l'on ne peut pas vraiment calculer avec les infinis.

Dans ton exemple, considérons l'équation NQ=Q (où on suppose que N>1). Elle est équivalente à (N-1)Q=0, et la seule solution algébrique est Q=0. Si ∞ était aussi une solution, on aurait une contradiction car, d'une part, on aurait que (N-1)∞=0 mais, d'autre part, l'infini multiplié par un nombre non nul reste l'infini, c.-à-d. que (N-1)∞=∞. Il en découlerait que 0=∞ ce qui est contradictoire.

De façon générale, on ne peut même pas vraiment dire que ∞=∞ puisque ∞-∞ n'est pas égal à zéro, c'est ce qu'on appelle une forme indéterminée. Ceci indique que non seulement l'infini n'est pas un nombre, mais qu'en plus il n'a même pas d'identité fixe.

Pour ce genre de raisons, réfléchir sur base de calculs approximatifs avec des infinis, c'est tomber rapidement dans des élucubrations insensées.

[Vanleers]

Mes allusions aux tiroirs et aux commerçants de points auraient du vous suggérer de prendre mon message cum grano salis.

[jean tardieu]

Cum grano salis, on a bien le droit de galéjer, sans doute ! Surtout avec les infinis qui n'en finissent pas !

[Vanleers]

Je signale un lien intéressant sur la question de l’infini en mathématiques en :

https://uel.unisciel.fr/mathematiques/logique1/logique1_ch09/co/apprendre_ch9_01.html

Je cite le passage suivant :

Infini potentiel, infini actuel
La solution [au paradoxe de Zénon : Achille et la tortue] trouvée par le philosophe Aristote dans l'Antiquité fut de distinguer deux sortes d'infini.
L'infini potentiel, ou infini en puissance que l'on utilise par exemple lorsqu'on dit "Pour tout entier, on peut en trouver un plus grand";
L'infini actuel qui consiste à accepter et à travailler avec une infinité d'objets, de nombres considérés comme disponibles en même temps, tels que l'infinité d'intervalles de temps et de distances envisagés dans l'exemple d'Achille ou pour prendre un exemple d'aujourd'hui, le fait de dire "soit l'ensemble des entiers...".
La solution trouvée par Aristote fut d'accepter des raisonnements faisant intervenir l'infini potentiel et de refuser l'infini actuel, en considérant qu'on n'en avait pas besoin en mathématiques.

L'infini en mathématiques
Le point de vue auquel se sont arrêtés les mathématiciens depuis l'Antiquité a, pour l'essentiel, été de refuser le débat. On évite d'introduire l'infini actuel, ensemble portant sur une infinité d'objets existant simultanément, et on se contente, y compris dans le calcul infinitésimal, de l'infini potentiel, en se donnant la possibilité d'augmenter ou de diminuer toute grandeur donnée. Classiquement, on peut dire qu'un point appartient à une droite, mais il est impossible de dire que la droite est constituée de points. Ceci sert de garde-fou après les querelles provoquées par l'usage de l'infini.

A la fin du XIX° siècle, avec Bolzano et Cantor, l’infini actuel a été explicitement introduit en mathématiques dans l’étude des ensembles infinis.
Par exemple, un segment de droite est considéré comme un ensemble infini de points.
De même, le carré construit sur ce segment est considéré, lui aussi, comme un ensemble infini de points et il est facile, comme déjà indiqué dans un post précédent, de construire une bijection entre ces deux ensembles qui fait correspondre à tout point du segment un point du carré et un seul, et réciproquement; ce qui démontre que ces deux ensembles ont la même puissance.

Resterait à savoir si l’introduction de l’infini actuel en mathématiques a un intérêt dans une approche philosophique plus générale du monde.

[neopilina]

Infini potentiel, infini actuel
La solution [au paradoxe de Zénon : Achille et la tortue] trouvée par le philosophe Aristote dans l'Antiquité fut de distinguer deux sortes d'infini.
L'infini potentiel, ou infini en puissance que l'on utilise par exemple lorsqu'on dit "Pour tout entier, on peut en trouver un plus grand";
L'infini actuel qui consiste à accepter et à travailler avec une infinité d'objets, de nombres considérés comme disponibles en même temps, tels que l'infinité d'intervalles de temps et de distances envisagés dans l'exemple d'Achille ou pour prendre un exemple d'aujourd'hui, le fait de dire "soit l'ensemble des entiers...".
La solution trouvée par Aristote fut d'accepter des raisonnements faisant intervenir l'infini potentiel et de refuser l'infini actuel, en considérant qu'on n'en avait pas besoin en mathématiques.

L'infini en mathématiques
Le point de vue auquel se sont arrêtés les mathématiciens depuis l'Antiquité a, pour l'essentiel, été de refuser le débat. On évite d'introduire l'infini actuel, ensemble portant sur une infinité d'objets existant simultanément, et on se contente, y compris dans le calcul infinitésimal, de l'infini potentiel, en se donnant la possibilité d'augmenter ou de diminuer toute grandeur donnée. Classiquement, on peut dire qu'un point appartient à une droite, mais il est impossible de dire que la droite est constituée de points. Ceci sert de garde-fou après les querelles provoquées par l'usage de l'infini.

Merci beaucoup Vanleers. Rien que je ne sache depuis trente ans et que je ne dise depuis plus de dix ans (depuis ma connexion à internet en aout 2009), mais ce n'est pas grave, c'est rafraîchir la mémoire des anciens et informer les nouveaux et c'est donc très bien dit, résumé.

A la fin du XIX° siècle, avec Bolzano et Cantor, l’infini actuel a été explicitement introduit en mathématiques dans l’étude des ensembles infinis.
Par exemple, un segment de droite est considéré comme un ensemble infini de points.
De même, le carré construit sur ce segment est considéré, lui aussi, comme un ensemble infini de points et il est facile, comme déjà indiqué dans un post précédent, de construire une bijection entre ces deux ensembles qui fait correspondre à tout point du segment un point du carré et un seul, et réciproquement; ce qui démontre que ces deux ensembles ont la même puissance.

A titre personnel, je connais Cantor uniquement via ses travaux sur Zénon. Tel que tu le formules ci-dessus, l'introduction d'infinis actuels en mathématiques ne semble pas problématique, pourtant, un camarade également très compétent, Leonhard, signale ci-dessus :

Vous êtes nombreux à avoir fait des calculs avec l'infini. Mais il faut savoir que d'un point de vue algébrique, l'ajout des infinis exige de renoncer à des propriétés algébriques classiques, avec pour conséquence que l'on ne peut pas vraiment calculer avec les infinis.

Dans ton [Vanleers] exemple, considérons l'équation NQ=Q (où on suppose que N supérieur à 1). Elle est équivalente à (N-1)Q=0, et la seule solution algébrique est Q=0. Si ∞ était aussi une solution, on aurait une contradiction car, d'une part, on aurait que (N-1)∞=0 mais, d'autre part, l'infini multiplié par un nombre non nul reste l'infini, c.-à-d. que (N-1)∞=∞. Il en découlerait que 0=∞ ce qui est contradictoire.

De façon générale, on ne peut même pas vraiment dire que ∞=∞ puisque ∞-∞ n'est pas égal à zéro, c'est ce qu'on appelle une forme indéterminée. Ceci indique que non seulement l'infini n'est pas un nombre, mais qu'en plus il n'a même pas d'identité fixe.

Pour ce genre de raisons, réfléchir sur base de calculs approximatifs avec des infinis, c'est tomber rapidement dans des élucubrations insensées.

A propos de ceci :

Resterait à savoir si l’introduction de l’infini actuel en mathématiques a un intérêt dans une approche philosophique plus générale du monde.

Je le dirais autrement, je m'en expliquerais ci-dessous : l'examen de l'infini a t-il un intérêt philosophique ? " Toutes les routes mènent à Rome ", en clair, pas question de me priver a priori d'une possibilité (elles sont trop rares) avant de l'avoir creusé autant que je le peux et malheureusement, ici, mes capacités extrêmement limitées en mathématiques conditionnent, grèvent, mes recherches, et pourtant celles-ci, " mes interrogations sur l'infini via les mathématiques ", menées ontologiquement et donc dialectiquement, ne se sont pas montrées infructueuses (je l'ai dit, je songe à rendre accessible, public, mes " brouillons " à ce sujet).

Leonhard nous rappelle qu'il y a des géométries non-euclidiennes (je le savais, mais rien de plus), mais il nous montre aussi sur un autre fil qu'il y a plusieurs logiques formelles, et ça, je ne le savais pas. Mais c'est bien, ça ne me dérange pas, bien au contraire, cela renforce mon approche, qui est celle-ci : le problème, les modalités, des formalisations et des verbalisations (force est de constater que tous les H. sapiens ne parlent pas la même langue, variété des discours spécialisés, les sciences de la nature et les sciences humaines ne s'occupant du même type d'objet n'ont pas la même épistémologie, etc.), en soi : à partir de quoi, comment, avec quoi, etc., formalise t-on ? Qu'est-ce qu'une formalisation, une verbalisation, une esthétique, on va dire " un Discours " ? C'est une tentative réglée de dire ce qui est, vaut, fait sens (sciences de la nature) et/ou Sens (éthologie et sciences humaines). L'éléate le formule ainsi : comment passe t-on de l'Être, infini ontologique et potentiel (1), à tel ou tel Etant, un et Un : signifiant. Et tous : des plus basiques, mes sensations, perceptions, d'être vivant voire de Sujet, etc., et ce jusqu'aux plus élaborés, formalisés, rigoureux (sciences, mathématiques, logiques formelles, verbalisations).

Sur ce forum, je ne sais plus quand ni où (!), j'ai déjà fait la liste, certainement non-exhaustive, des spécialistes, qui, " un jour ", sous une forme ou une autre, finissent par se heurter, par trébucher, rencontrer, etc., l'infini. Dans cette liste, il y avait aussi bien le philosophe, le métaphysicien, le théologien, le moraliste, que le physicien, le cosmologiste, le mathématicien, etc., etc., ça commence à faire beaucoup, etc., enfin bref, je résume à titre personnel : on ne peut pas faire l'économie ou encore faire l'impasse sur ce thème. Tous ceux qui se proposent, chacun à leur façon spécifique, de remonter " à la source " pour pouvoir y puiser puis le dire, tant bien que mal, rencontrent l'infini sur leur " Chemin ". A quoi et comment donne t-on forme : définition aussi radicale que possible, en tous cas pour moi, de l'épistémologie.

A la fin du XIX° siècle, avec Bolzano et Cantor, l’infini actuel a été explicitement introduit en mathématiques dans l’étude des ensembles infinis.
Par exemple, un segment de droite est considéré comme un ensemble infini de points.

Un petit " peu " éléate sur les bords, pour le dire ainsi, il se trouve, ainsi, que je suis notoirement allergique aux infinis actuels, en acte. Ci-dessus par exemple, tu considères qu'un segment de droite est un infini en acte. Je ne suis pas d'accord : ce qui serait un infini en acte, c'est le dénombrement en acte, effectif (désolé !), actualisé, de tous les points qui constituent ce segment : du point de vue du nombre de points qui composent ce segment, celui-ci reste un infini potentiel !!

(1) Je ne sais plus qui, hks, Vanleers, ou un autre avait posté cet article, il m'a beaucoup stimulé et amené à relire des passages encore pertinents de la " Physique " d'Aristote :  " Aristote admet-il un infini en acte et en puissance en " Physique III, 4 " ? par Antoine Côté :

https://www.persee.fr/doc/phlou_0035-3841_1990_num_88_80_6649

[Magni]

Je ne suis pas d'accord avec la formulation qui dit que l'infini mathématique est un infini en acte. Il existe des infinis potentiels, on n'a jamais découvert d'infini en acte.

Le potentiel est métaphysique, l'acte est physique. De quel droit peut on utiliser le vocabulaire aristotélicien dans un sens non aristotélicien ?

Il n'existe pas d'action métaphysique, il n'y a pas de causalité métaphysique.
Ce qui est action et qui engendre une réaction, appartient au monde physique.
Il n'existe pas d'ensemble purement mathématique "en acte". Ce qui est purement mathématique et purement potentiel et non actuel.

L'infini en mathématique est un infini en puissance.
La fonction d'onde stipule que le photon pourrait, en puissance, être localisé dans une infinité d'endroit, mais en acte, il n'est localisé que dans un seul endroit à la fois.
Cela pèse combien de Newton l'ensemble des entier ? Quelle action cela peut il avoir dans une relation causale ?

"Prendre l'ensemble des entiers" est un abus de langage, on ne prend rien et les entiers restent où ils sont.

On aura un infini en acte quand on aura trouvé l'infini dans le monde physique.

[Leonhard]

Introduire un infini actuel n'est pas si difficile à accepter que cela. Pour ce faire, il suffit de méditer sur le fait que l'on peut désigner en acte des possibilités.

Exemple :

Disons qu'une expression numérique est une suite finie de chiffres (pris parmi "0", "1", "2", ..., "9"). Voici quelques expressions numériques :

• 829039
  
• 3738
  
• 45678923847

Il est clair qu'il y a une infinité de possibilités. Décidons alors de désigner par la lettre N l'ensemble de toutes les expressions numériques possibles. Et tout de suite, comme par magie, nous avons créé un symbole, "N", qui désigne en un coup un ensemble infini. Il s'agit essentiellement de l'ensemble des nombres appelés "naturels".

L'opération ci-dessus n'a l'air de rien mais elle est d'une puissance folle. Elle est une application d'un axiome fondamental de la théorie des ensembles, l'axiome de compréhension. Cet axiome dit que si l'on a une propriété P(x) portant sur un objet x d'un certain type, alors on peut toujours parler de l'ensemble de tous les objets de ce type qui possèdent cette propriété.

Dans l'exemple ci-dessus, les objets sont des expressions (des suites finies de symboles). La propriété P(x) que j'ai introduite est "x contient exclusivement des chiffres". L'axiome de compréhension me permet alors de parler de l'ensemble de toutes les expressions qui possèdent cette propriété, c'est-à-dire de toutes les expressions numériques. Et comme il y en a une infinité, je peux donc parler, de façon effective et actuelle, de cette infinité, et je l'ai même dénotée par la lettre N.

Cela signifie que la propriété P(x) me permet non seulement de définir N, mais également de décider si une expression quelconque x appartient à N ou pas. La propriété P(x), qui n'est rien d'autre qu'une simple phrase, est tout ce qu'il me faut pour travailler avec l'ensemble infini N. Dans le jargon, cette propriété P(x) est appelée une caractérisation de l'ensemble N et l'on a que :

x appartient à N si et seulement si P(x) est vrai.

La moralité de l'histoire, est que pour travailler en acte avec des ensembles infinis, tout ce qu'il faut, c'est un langage qui nous donne la possibilité de les désigner. Car, au fond, on ne fait rien d'autre en mathématiques que parler de choses : on ne les manipule pas avec nos mains, on ne les perçoit pas avec nos sens. Et si les mathématiciens travaillent depuis longtemps avec des infinis achevés, c'est grâce à leur langage. Et ce langage prend la forme d'une théorie axiomatique, ce que les logiciens connaissent fort bien.

Certains peuvent trouver qu'un tel tour de passe-passe linguistique est superficiel, mais qu'ils se détrompent. Car une fois que j'ai défini mon ensemble N, je peux l'analyser, le manipuler, construire de nouveaux ensembles avec, etc. C'est ainsi qu'à partir de l'ensemble N des nombres naturels, je peux construire l'ensemble Z est entiers, des rationnels, des réels, des complexes, ainsi que définir des fonctions sur ces ensembles, ce qui engendre toute l'algèbre, l'analyse, la géométrie, etc.

Ceci n'est qu'un premier pas vers la conception dite formaliste des mathématiques, qui s'oppose fameusement à la conception platonicienne ou réaliste.

[hks]

Je ne suis pas d'accord avec la formulation qui dit que l'infini mathématique est un infini en acte. Il existe des infinis potentiels, on n'a jamais découvert d'infini en acte.

Certes,  si "en acte" c'est l'actuel.
L'actuel est déterminé.

[Bergame]

Certains peuvent trouver qu'un tel tour de passe-passe linguistique est superficiel, mais qu'ils se détrompent. Car une fois que j'ai défini mon ensemble N, je peux l'analyser, le manipuler, construire de nouveaux ensembles avec, etc. C'est ainsi qu'à partir de l'ensemble N des nombres naturels, je peux construire l'ensemble Z est entiers, des rationnels, des réels, des complexes, ainsi que définir des fonctions sur ces ensembles, ce qui engendre toute l'algèbre, l'analyse, la géométrie, etc.

Tu as décidément tendance à te laisser prendre aux pièges du langage, Leonhard. Mais ce n'est pas parce qu'on peut désigner un ensemble infini qu'il devient un infini en acte. Dire que "N" désigne un infini en acte, c'est un peu confondre le mot "lapin" (qui désigne lui aussi une infinité d'exemplaires de lapins réels, mort, vivants, ou à venir) avec ce lapin-ci, blanc et noir, que je croise par inadvertance dans les sous-bois. Bref, une confusion évidente entre le signifiant et le signifié.

Et bien sûr, tu peux construire ce que tu veux, avec le langage, en agençant les mots pour faire des jeux de langage, créer des chimères, etc.  Et en particulier avec le langage mathématique : Aujourd'hui, on construit des objets à n dimensions, en mathématiques, des objets à une infinité de dimensions. Certes, ils existent en puissance, virtuellement, mais existent-ils en acte ?

[Vanleers]

A la fin du XIX° siècle, avec Bolzano et Cantor, l’infini actuel a été explicitement introduit en mathématiques dans l’étude des ensembles infinis.
Par exemple, un segment de droite est considéré comme un ensemble infini de points.

Un petit " peu " éléate sur les bords, pour le dire ainsi, il se trouve, ainsi, que je suis notoirement allergique aux infinis actuels, en acte. Ci-dessus par exemple, tu considères qu'un segment de droite est un infini en acte. Je ne suis pas d'accord : ce qui serait un infini en acte, c'est le dénombrement en acte, effectif (désolé !), actualisé, de tous les points qui constituent ce segment : du point de vue du nombre de points qui composent ce segment, celui-ci reste un infini potentiel !!

Ce que je crois comprendre, c’est que l’infini en acte serait, selon vous, la construction de l’ensemble des points du segment de droite par dénombrement.
Or, Cantor a démontré que l’ensemble des points d’un segment de droite n’est pas dénombrable : c’est le célèbre argument de la diagonale.
Il faudrait donc trouver autre chose que le dénombrement pour construire  le segment de droite.

Dans le même ordre d’idées, j’ai critiqué, à ma façon, la construction erronée du carré par empilement de N rectangles de hauteur 1/N en faisant tendre N vers l’infini.
Pour une partition donnée du carré, l’ordonnée de la limite supérieure de chaque rectangle est égale à n/N avec 1≤ n entier ≤ N
n/N est un nombre rationnel (quotient de 2 entiers) et quand N tend vers l’infini (infini potentiel), chaque rectangle tend vers un segment dont l’ordonnée est rationnelle.
Le carré serait donc un ensemble de segments dont l’ordonnée est rationnelle, ce qui est faux car cet ensemble n’est qu’un sous-ensemble des segments que contient le carré, chaque segment ayant pour ordonnée un nombre réel.
L’ensemble des segments qui constituent un carré n’est pas dénombrable.

[jean tardieu]

On pourrait dire que la physique tient pour assuré ce qu'elle constate, sous le contrôle des mathématiques.
La philosophie tient pour assuré tout ce qui lui passe par la tête (Dieu...l'infini... le véganisme... et autres joyeusetés...))

[Contenu sponsorisé]