L'infini est-il limité ?
+7
quid
hks
Vanleers
neopilina
Magni
jean tardieu
Leonhard
11 participants
Page 6 sur 9
Page 6 sur 9 •  1, 2, 3, 4, 5, 6, 7, 8, 9
1, 2, 3, 4, 5, 6, 7, 8, 9 
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
https://www.cairn.info/revue-de-metaphysique-et-de-morale-2011-2-page-203.htmLeibniz a écrit:Non obstant mon Calcul Infinitesimal, je n’admets point de veritable nombre infini, quoyque je confesse que la multitude des choses passe tout nombre fini, ou plustôt tout nombre. […] Le Calcul infinitesimal est utile, quand il s’agit d’appliquer la Mathematique à la Physique, cependant ce n’est point par là que je pretends rendre compte de la nature des choses. Car je considere les quantités infinitesimales comme des fictions utiles.
(À Masson, 1716, GP VI, 629. .)
37Et c’est pourquoi il n’hésitera pas à moquer ceux qui, à l’instar de Fontenelle, entendaient en tirer quelques éléments métaphysiques :
38
Entre nous je crois que Mons. de Fontenelle, qui a l’esprit galant et beau, en a voulu railler, lorsqu’il a dit qu’il vouloit faire des elemens metaphysiques de nostre calcul. Pour dire le vray, je ne suis pas trop persuadé moy même, qu’il faut considerer nos infinis et infiniment petits autrement que comme des choses ideales ou comme des fictions bien fondées. Je croy qu’il n’y a point de creature au dessous de laquelle il n’y ait une infinité de creatures, cependant je ne crois point qu’il y en ait, ny même qu’il y en puisse avoir d’infiniment petites et c’est ce que je crois pouvoir demonstrer.
hks- Digressi(f/ve)

- Nombre de messages : 12518
Date d'inscription : 04/10/2007
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
hks > Une branche des mathématiques, l'analyse non standard, a formalisé rigoureusement les infiniment petits (et les infiniment grands) de Leibniz :
https://fr.wikipedia.org/wiki/Analyse_non_standard
Cela fait donc maintenant officiellement et rigoureusement partie des maths.
https://fr.wikipedia.org/wiki/Analyse_non_standard
Cela fait donc maintenant officiellement et rigoureusement partie des maths.
Leonhard- Digressi(f/ve)

- Nombre de messages : 194
Date d'inscription : 03/09/2007
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Ce n'est pas en s'adressant à ma personne en disant que je suis mal construit que cela va déconstruire mes arguments.
Je connais suffisamment les rudiments pour savoir que la "formule de Leibniz-Grégory" à pour solution le nombre Pi.
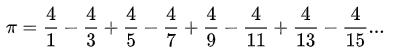
Et oui, à chaque fois qu'on fait une itération, on coupe en deux le domaine d'incertitude, et c'est de cela dont on parle.
Et d'accord pour ceci:
Mais cela, je dis que c'est faux :
L'infini n'est toujours pas achevé, et vous n'avez absolument pas la valeur de 3-Pi, pas plus que je n'ai la valeur de Pi.
Sérieusement, je me fout que Cantor (mais je croyais que c'était plutôt un des ses disciples) ait baptisé un truc nouveau avec ce nom de "infini actuel", mais le problème c'est que c'est le même infini qu'on trouve dans Achille et la tortue dont l'itération coupe le domaine en deux à chaque fois et à l'époque, ce truc s'appelait "infini potentiel", et vous semblez vouloir ignorer ce problème, vous ne situez pas l'infini actuel de Cantor par rapport à l'infini potentiel d'Aristote alors que c'est manifestement pareil pour moi. Pensez vous que c'est pareil ou différent ? Vous faites comme si vous n'aviez pas besoin de montrer que vous avez conscience de ce problème.
Vous pouvez ignorer Aristote si vous voulez, peu importe. Parlons d'autre chose.
J'ai raté quoi, il est où le nombre 3-Pi, vous pouvez vraiment faire l'opération qui donne ce résultat en un claquement de doigt ?
A ce stade je ne suis toujours pas convaincu, je ne vous crois pas, montrez moi !
Combien vaut 3-Pi ?
Je connais suffisamment les rudiments pour savoir que la "formule de Leibniz-Grégory" à pour solution le nombre Pi.
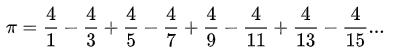
Et oui, à chaque fois qu'on fait une itération, on coupe en deux le domaine d'incertitude, et c'est de cela dont on parle.
Leonhard a écrit:
Par construction, chaque IN est contenu dans IN-1, donc on a bien une suite d'intervalles emboîtés. De plus, la largeur de ces intervalles tend vers 0 (puisqu'elle est divisée par deux à chaque étape).
Et d'accord pour ceci:
Leonhard a écrit:Dans la suite des IN, un seul élément appartient à tous ces intervalles sans exception : c'est pi-3. Voilà pourquoi l'intersection le contient comme unique élément.
Mais cela, je dis que c'est faux :
Leonhard a écrit:Oui, en mathématiques, on peut faire une opération (ici, l'intersection) sur une infinité d'objets d'un coup, en un claquement de doigt.
L'infini n'est toujours pas achevé, et vous n'avez absolument pas la valeur de 3-Pi, pas plus que je n'ai la valeur de Pi.
Sérieusement, je me fout que Cantor (mais je croyais que c'était plutôt un des ses disciples) ait baptisé un truc nouveau avec ce nom de "infini actuel", mais le problème c'est que c'est le même infini qu'on trouve dans Achille et la tortue dont l'itération coupe le domaine en deux à chaque fois et à l'époque, ce truc s'appelait "infini potentiel", et vous semblez vouloir ignorer ce problème, vous ne situez pas l'infini actuel de Cantor par rapport à l'infini potentiel d'Aristote alors que c'est manifestement pareil pour moi. Pensez vous que c'est pareil ou différent ? Vous faites comme si vous n'aviez pas besoin de montrer que vous avez conscience de ce problème.
Vous pouvez ignorer Aristote si vous voulez, peu importe. Parlons d'autre chose.
J'ai raté quoi, il est où le nombre 3-Pi, vous pouvez vraiment faire l'opération qui donne ce résultat en un claquement de doigt ?
A ce stade je ne suis toujours pas convaincu, je ne vous crois pas, montrez moi !
Combien vaut 3-Pi ?
_________________
Ce que je dis n'engage que moi.

Magni- Digressi(f/ve)

- Nombre de messages : 1065
Localisation : 62100
Date d'inscription : 03/05/2016
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Leonhard a écrit:L'intersection entre deux ensembles A et B, c'est l'ensemble constitué des éléments contenus à la fois dans A et dans B.
L'intersection d'une infinité d'ensembles IN, c'est l'ensemble constitué des éléments contenus dans tous les ensembles IN, pour tous les N (et il y en a une infinité).
Désolé, je ne comprends toujours pas.
Quel que soit N, aussi grand soit-il, les segments étant emboîtés les uns dans les autres, l’intersection de I1, I2, I3, … IN est IN c’est-à-dire un ensemble infini.
Vanleers- Digressi(f/ve)

- Nombre de messages : 4217
Date d'inscription : 15/01/2017
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Il est vrai que I1 ∩ I2 ∩ I3 ∩ ... ∩ IN = IN. Mais ce n'est là que l'intersection d'un nombre fini d'intervalles, puisque le dernier est IN.
Or, il y a une infinité de IN. Ce qu'on prend, c'est l'intersection de tous les IN. C'est donc l'intersection d'une infinité d'intervalles :
I1 ∩ I2 ∩ I3 ∩ ...
et cette expression n'a pas de fin.
https://fr.wikipedia.org/wiki/Intersection_(math%C3%A9matiques)#Intersection_d'une_famille_d'ensembles
Or, il y a une infinité de IN. Ce qu'on prend, c'est l'intersection de tous les IN. C'est donc l'intersection d'une infinité d'intervalles :
I1 ∩ I2 ∩ I3 ∩ ...
et cette expression n'a pas de fin.
https://fr.wikipedia.org/wiki/Intersection_(math%C3%A9matiques)#Intersection_d'une_famille_d'ensembles
Leonhard- Digressi(f/ve)

- Nombre de messages : 194
Date d'inscription : 03/09/2007
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Il est évidemment impossible de donner concrètement toutes les décimales de pi, puisqu'il y en a une infinité. C'est déjà le cas pour 1/3. Personne ne prétend pouvoir accomplir ce qui est impossible dans notre réalité concrète.Magni a écrit:J'ai raté quoi, il est où le nombre 3-Pi, vous pouvez vraiment faire l'opération qui donne ce résultat en un claquement de doigt ?
A ce stade je ne suis toujours pas convaincu, je ne vous crois pas, montrez moi !
Cela dit, déterminer les décimales d'un nombre n'est qu'une façon d'appréhender ce nombre. Une façon très limitée, d'ailleurs, que l'on s'emploie à dépasser dès l'école secondaire. Car les maths ont depuis longtemps développé de nombreux autres moyens de parler, avec une précision totale, des nombres.
Tu sembles prendre pour acquis la formule de Leibniz :
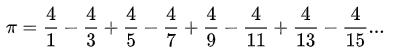
Mais tu devrais t'interroger sur cette formule. Car s'il est impossible d'écrire toutes les décimales de pi, cela semble signifier que personne au monde, ni dans l'univers, ne sait exactement ce qu'est le nombre pi. Mais si c'était vraiment le cas, comment expliquer que l'on puisse affirmer que pi soit strictement égal à quoi que ce soit, comme dans la formule de Leibniz ? Comment peut-on affirmer une égalité stricte entre pi et un autre nombre, s'il est impossible de vérifier que toutes les décimales sont les mêmes ? Supposer l'hypothèse que j'ai soulignée t'amène à cette aporie.
Il faut donc en conclure que l'hypothèse soulignée doit être rejetée, puisqu'elle mène à une aporie. Autrement dit : même s'il est impossible d'écrire toutes les décimales de pi, nous avons d'autres moyens d'accéder avec une stricte précision à pi. Ces autres moyens, ce sont, de façon générale, les théorèmes mathématiques portant sur pi. Tous ces théorèmes sont démontrés en un nombre fini d'étapes et nous sont accessibles.
C'est comme ça que les mathématiques arrivent à dire des choses strictement précises et vraies sur des choses liées à l'infini, comme les nombres transcendants, les ensembles infinis, etc. : elles font usages de concepts et de démonstrations, au lieu de se cantonner au vulgaire et basique calcul arithmétique.
Si tu réfléchis à la formule de Leibniz, tu te rendras compte du miracle accompli : dire que pi, un nombre apparemment à jamais inaccessible, est strictement égal à une expression certes de longueur infinie, mais dont la structure est parfaitement claire. On a réussi à appréhender pi. Bienvenue dans les mathématiques.
Leonhard- Digressi(f/ve)

- Nombre de messages : 194
Date d'inscription : 03/09/2007
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Petite réflexion qui n'engage que moi.
C'est quoi un nombre réel ?
(Je sais, c'est trivial)
Prenons un mètre étalon et utilisons le pour mesurer une planche par exemple.
Si l'on peut reporter 3 fois le mètre étalon et qu'il reste un bout de planche inférieur au mètre, on peut dire que la planche mesure entre 3 et 4 mètres et s'en tenir là, ou vouloir avoir une mesure un peu plus précise. En divisant le mètre étalon en 10, en le graduant, on va pourvoir préciser le restant de la planche à la dizaine de centimètre prés. On trouvera alors une mesure par exemple entre 3.6 m et 3.7 m. En divisant encore la chaque graduation par dix on va décendre au centimètre et trouver par exemple une mesure entre 3.62 m et 3.63 m. Et ainsi de suite.
Un nombre réel est en fait une mesure. Un nombre entier est plus une quantité.
On a l'habitude d'assimiler les deux, mais c'est peut-être un excès.
Le nombre réel c'est par exemple la mesure théoriquement exact de la planche.
Or en terme de mesure, l'exactitude n'existe pas. le nombre réel correspondant à la taille de la planche est en fait quelque chose d'inventé, d'abstrait. En réalité un tel nombre n'existe pas il n'y a pas de nombre exact correspondant à la taille de la planche, on a toujours qu'une approximation, car mesurer au plus précis n'a pas de fin.
C'est tout aussi juste comme le dit Magni de dire Pi = 4/1 - 4/3 + 4/5 - 4/7 + 4/9 - 4/11 + 4/13 - 4/15 ... que Pi = 3,141592653589793... . De toute manière, on a une précision qui demande un développement infini pour obtenir l'exactitude, c'est à dire le nombre réel.
Tant que l'on considère une mesure, cela s'applique aussi a des nombres supposés entiers. On ne peut pas pointer avec précision sur la planche l'emplacement correspondant à exactement 1 (un) mètre. Il y aura toujours à un moment un écart infinitésimal avec la valeur 1. On aura par exemple 1.000000000000000000001 ou 0.999999999999999999998. La mesure exacte demande une précision infinie. C'est pour cela qu'un nombre réel est une abstraction.
La mesure exacte étant l'abstraction numérique exacte d'une position, cela ne veut pas dire qu'un emplacement sur une planche n'a pas la position qu'elle occupe, c'est seulement que cela ne peut pas être, à part de manière abstraite à l'aide de la notion de nombre réel, mis en correspondance avec une quantité numérique exacte au sens classique.
Le fait que les nombres réels permettent de couvrir une continuité est en définitive plus un axiome que quelque chose qui se démontrerait. Les nombres réels sont introduits justement pour assurer la continuité numérique, pour traiter mathématiquement du continu.
------
Mais effectivement on peut en mathématique trouver des formules qui réduisent le calcul itératif :

C'est quoi un nombre réel ?
(Je sais, c'est trivial)
Prenons un mètre étalon et utilisons le pour mesurer une planche par exemple.
Si l'on peut reporter 3 fois le mètre étalon et qu'il reste un bout de planche inférieur au mètre, on peut dire que la planche mesure entre 3 et 4 mètres et s'en tenir là, ou vouloir avoir une mesure un peu plus précise. En divisant le mètre étalon en 10, en le graduant, on va pourvoir préciser le restant de la planche à la dizaine de centimètre prés. On trouvera alors une mesure par exemple entre 3.6 m et 3.7 m. En divisant encore la chaque graduation par dix on va décendre au centimètre et trouver par exemple une mesure entre 3.62 m et 3.63 m. Et ainsi de suite.
Un nombre réel est en fait une mesure. Un nombre entier est plus une quantité.
On a l'habitude d'assimiler les deux, mais c'est peut-être un excès.
Le nombre réel c'est par exemple la mesure théoriquement exact de la planche.
Or en terme de mesure, l'exactitude n'existe pas. le nombre réel correspondant à la taille de la planche est en fait quelque chose d'inventé, d'abstrait. En réalité un tel nombre n'existe pas il n'y a pas de nombre exact correspondant à la taille de la planche, on a toujours qu'une approximation, car mesurer au plus précis n'a pas de fin.
C'est tout aussi juste comme le dit Magni de dire Pi = 4/1 - 4/3 + 4/5 - 4/7 + 4/9 - 4/11 + 4/13 - 4/15 ... que Pi = 3,141592653589793... . De toute manière, on a une précision qui demande un développement infini pour obtenir l'exactitude, c'est à dire le nombre réel.
Tant que l'on considère une mesure, cela s'applique aussi a des nombres supposés entiers. On ne peut pas pointer avec précision sur la planche l'emplacement correspondant à exactement 1 (un) mètre. Il y aura toujours à un moment un écart infinitésimal avec la valeur 1. On aura par exemple 1.000000000000000000001 ou 0.999999999999999999998. La mesure exacte demande une précision infinie. C'est pour cela qu'un nombre réel est une abstraction.
La mesure exacte étant l'abstraction numérique exacte d'une position, cela ne veut pas dire qu'un emplacement sur une planche n'a pas la position qu'elle occupe, c'est seulement que cela ne peut pas être, à part de manière abstraite à l'aide de la notion de nombre réel, mis en correspondance avec une quantité numérique exacte au sens classique.
Le fait que les nombres réels permettent de couvrir une continuité est en définitive plus un axiome que quelque chose qui se démontrerait. Les nombres réels sont introduits justement pour assurer la continuité numérique, pour traiter mathématiquement du continu.
------
Tout à fait. Le calcul comme l'écriture décimale du nombre Pi demandent un développement infini. Cependant, l'expression mathématique de Pi en dit un peu plus sur Pi que sa simple écriture décimale.Leonhard a écrit:Si tu réfléchis à la formule de Leibniz, tu te rendras compte du miracle accompli : dire que pi, un nombre apparemment à jamais inaccessible, est strictement égal à une expression certes de longueur infinie, mais dont la structure est parfaitement claire. On a réussi à appréhender pi. Bienvenue dans les mathématiques.
Sur ce que j'ai souligné : Je pense qu'il y a une inversion du concept d'infini. Notamment pour les nombre réels. L'infini n'est pas dans la position dans le continu : Quand on coupe une planche, elle aura une taille bien précise empiriquement parlant. L'infini n'arrive que lorsque l'on tente d'appréhender à l'aide d'un nombre, la taille de la planche. C'est uniquement une problématique mathématique et non pas l'appréhension d'un quelconque infini en fait.Leonhard a écrit:C'est comme ça que les mathématiques arrivent à dire des choses strictement précises et vraies sur des choses liées à l'infini, comme les nombres transcendants, les ensembles infinis, etc. : elles font usages de concepts et de démonstrations, au lieu de se cantonner au vulgaire et basique calcul arithmétique.
Mais effectivement on peut en mathématique trouver des formules qui réduisent le calcul itératif :


quid- Digressi(f/ve)

- Nombre de messages : 1080
Date d'inscription : 04/08/2012
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Leonhard a écrit:Il est évidemment impossible de donner concrètement toutes les décimales de pi, puisqu'il y en a une infinité. C'est déjà le cas pour 1/3. Personne ne prétend pouvoir accomplir ce qui est impossible dans notre réalité concrète.Magni a écrit:J'ai raté quoi, il est où le nombre 3-Pi, vous pouvez vraiment faire l'opération qui donne ce résultat en un claquement de doigt ?
A ce stade je ne suis toujours pas convaincu, je ne vous crois pas, montrez moi !
Cela dit, déterminer les décimales d'un nombre n'est qu'une façon d'appréhender ce nombre. Une façon très limitée, d'ailleurs, que l'on s'emploie à dépasser dès l'école secondaire. Car les maths ont depuis longtemps développé de nombreux autres moyens de parler, avec une précision totale, des nombres.
Tu sembles prendre pour acquis la formule de Leibniz :
Mais tu devrais t'interroger sur cette formule. Car s'il est impossible d'écrire toutes les décimales de pi, cela semble signifier que personne au monde, ni dans l'univers, ne sait exactement ce qu'est le nombre pi. Mais si c'était vraiment le cas, comment expliquer que l'on puisse affirmer que pi soit strictement égal à quoi que ce soit, comme dans la formule de Leibniz ? Comment peut-on affirmer une égalité stricte entre pi et un autre nombre, s'il est impossible de vérifier que toutes les décimales sont les mêmes ? Supposer l'hypothèse que j'ai soulignée t'amène à cette aporie.
Il faut donc en conclure que l'hypothèse soulignée doit être rejetée, puisqu'elle mène à une aporie. Autrement dit : même s'il est impossible d'écrire toutes les décimales de pi, nous avons d'autres moyens d'accéder avec une stricte précision à pi. Ces autres moyens, ce sont, de façon générale, les théorèmes mathématiques portant sur pi. Tous ces théorèmes sont démontrés en un nombre fini d'étapes et nous sont accessibles.
C'est comme ça que les mathématiques arrivent à dire des choses strictement précises et vraies sur des choses liées à l'infini, comme les nombres transcendants, les ensembles infinis, etc. : elles font usages de concepts et de démonstrations, au lieu de se cantonner au vulgaire et basique calcul arithmétique.
Si tu réfléchis à la formule de Leibniz, tu te rendras compte du miracle accompli : dire que pi, un nombre apparemment à jamais inaccessible, est strictement égal à une expression certes de longueur infinie, mais dont la structure est parfaitement claire. On a réussi à appréhender pi. Bienvenue dans les mathématiques.
Oui la formule de Gottfried Wilhelm Leibniz est parfaitement valable et dument démontrée, je me suis déjà interrogé sur cette question pour répondre à votre question sur ma vie personnelle (j'adore qu'on s'intéresse à moi), ce genre de curiosité m'intéresse. Et je savais déjà qu'on ne peut pas calculer un nombre transcendant en écrivant son développement décimal infini, justement à cause du terme "infini".
Maintenant que vous dites qu'on n'aura jamais le résultat de la formule de Leibniz, vous avez compris de quoi je vous parle, il est temps de généraliser
Peut importe la formule disons qu'il existe des formules qui donnent des nombres transcendants qui se définissent par leur développement décimal infini (les transcendants ont un développement décimal aléatoire et non répétitif, et l'aléatoire mathématique n'a rien à voir avec le hasard, il est totalement défini.)
Il faut arrêter de dire qu'on peut opérer ces formules, aussi longtemps qu'on n'aura pas la puissance des Dieux, la puissance de notre claquement de doigt ne pourra pas achever l'infini.
On avait déjà réussit à appréhender Pi quand on l'a appelé Pi parce que c'est la première lettre de "périmètre" en Grec.
Pi est entièrement défini par son identité de rapport de longueur du périmètre divisé par la longueur du diamètre.
Certes c'est une équation géométrique, prenons un exemple arithmétique.
Peut importe le nom de la formule, ce qui compte c'est le processus de formalisation.
x= 2^(2^0,5))
Il a été démontré qu'on peut ainsi construire des nombres transcendants, les entiers élevés à une puissance non algébrique sont des nombres transcendants.
Vous pourrez trouver une suite pour calculer autant de chiffres après la virgule de x que vous voulez, mais vous ne pourrez pas calculer tous les termes d'une suite infinie.
Vous faites comment pour donner une valeur de x ?
Vous dites que calculer ses décimales n'est qu'une façon d'appréhender x, vous avez quoi comme autre façon ?
Le principe opératoire d'intersection d'ensembles qui se coupe par moitié à chaque itération ne permet que de calculer des chiffres après la virgule. Il n'y a pas d'autre méthode pour approcher un transcendant que d'en calculer des décimales.
Il y a des formules qui donnent l'identité des transcendants mais il n'y a pas de méthode qui permette de les calculer.
L'identité du nombre Pi c'est sa forme platonique, c'est métaphysique, c'est dans le domaine du potentiel c'est l'infini potentiel aristotélicien, ça on connaît depuis Aristote.
La valeur du nombre Pi, c'est son apparence en acte, sa réalité physique manipulable et utilisable en analyse.
Elle n'est pas infinie en acte, dans le monde physique on ne peut réaliser qu'une partie finie du nombre Pi.
Vous avez quand même le droit d'appeler "le cardinal de l'ensemble de tous les quotients algébriques qui s'additionnent dans la formule de Leibniz pour obtenir exactement Pi" un "infini actuel de Cantor", mais je conteste que ce soit l'infini actuel d'Aristote et je dis que c'est exactement le même infini et que ceux qui ne comprennent pas ça peuvent éventuellement confondre rêve et réalité.
Vous n'avez pas de fondement à dire que vous pouvez véritablement obtenir le résultat d'une formule géométrique ou arithmétique qui identifie un nombre transcendant, oui le résultat existe véritablement mais il reste dans un monde métaphysique et est au moins en partie hors de portée du genre humain en l'état actuelle des connaissances humaines.
_________________
Ce que je dis n'engage que moi.

Magni- Digressi(f/ve)

- Nombre de messages : 1065
Localisation : 62100
Date d'inscription : 03/05/2016
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Leonhard a écrit:Il est vrai que I1 ∩ I2 ∩ I3 ∩ ... ∩ IN = IN. Mais ce n'est là que l'intersection d'un nombre fini d'intervalles, puisque le dernier est IN.
Or, il y a une infinité de IN. Ce qu'on prend, c'est l'intersection de tous les IN. C'est donc l'intersection d'une infinité d'intervalles :
I1 ∩ I2 ∩ I3 ∩ ...
et cette expression n'a pas de fin.
https://fr.wikipedia.org/wiki/Intersection_(math%C3%A9matiques)#Intersection_d'une_famille_d'ensembles
L’intersection d’un nombre fini d’IN, c’est IN.
L’intersection d’un nombre infini d’IN, c’est IN lorsque N tend vers l’infini, c’est-à-dire un ensemble infini qui, quel que soit N aussi grand que l’on veut, a la puissance du continu.
Une façon de s’en sortir pourrait être la suivante.
Posons que le nombre Pi – 3, par exemple, existe. Appelons-le x.
Soit y un nombre différent de x.
S’il est différent de x, c’est que |y – x| = d avec d > 0
Quel que soit d, il existe N tel que la largeur de IN soit inférieure à d.
y ne sera pas dans IN et ceci est vrai pour tout nombre y.
Seul x peut rester dans l’intersection des IN.
CQFD ?
Je crains que non et que l’on ait le raisonnement suivant : si x existe alors x existe.
Perplexité.
Vanleers- Digressi(f/ve)

- Nombre de messages : 4217
Date d'inscription : 15/01/2017
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Mais je n'ai rien dit contre cette formalisation justifiée.Leonhard a écrit:hks > Une branche des mathématiques, l'analyse non standard, a formalisé rigoureusement les infiniment petits (et les infiniment grands) de Leibniz :
https://fr.wikipedia.org/wiki/Analyse_non_standard
Cela fait donc maintenant officiellement et rigoureusement partie des maths.

Ce n'est pas ce dont parle Leibniz. Leibniz traite d'une question,
en son temps, mais qui demeure toute à fait contemporaine;
Il s'agit du degré de réalité des infiniment petits .
Question posée aussi à l'infiniment grand puisque la réduction par divisions successives est potentiellement infiniment grande.Leibniz a écrit:je ne suis pas trop persuadé moy même, qu’il faut considerer nos infinis et infiniment petits autrement que comme des choses ideales ou comme des fictions bien fondées.
A la fin on a une vérité , le résultat; c'est un ceci posé; une vérité /un état de fait posé en tant que CQFD)
Mais l'opération est digne d'intérêt (l'opération au sens du travail effectué)
Si le résultat est posé statique
Il y eut néanmoins une progression. Le mathématicien déplace des pièces selon des règles et selon son imagination (comme le joueur d'échec).
Le mathématiciens commencent donc une manœuvre mentale et elle demeure dans le mental jusqu'au bout.
Mais il voudrait (peut- être
 ) nous persuader qu'elle sort du mental , à tout le moins que hors du mental on a (existe) la même réalité. La même sans différence de nature.
) nous persuader qu'elle sort du mental , à tout le moins que hors du mental on a (existe) la même réalité. La même sans différence de nature.C'est à dire nous convaincre, in fine, que la réalité de la nature est (au sens ontologique fort) une combinatoire mentale.
Par analogie, convaincre de l'identité de deux mondes: celui du rêve nocturne et celui de l'éveil diurne.
Dernière édition par hks le Mer 21 Avr 2021 - 10:24, édité 1 fois
hks- Digressi(f/ve)

- Nombre de messages : 12518
Localisation : Hauts de Seine
Date d'inscription : 04/10/2007
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
En gros oui, malgré que l'hypothèse soulignée n'ait rien à faire là. On ne pose pas que pi-3 existe, on sait qu'il existe. La question est de savoir s'il est le seul élément de l'intersection des IN.Vanleers a écrit:Une façon de s’en sortir pourrait être la suivante.
Posons que le nombre Pi – 3, par exemple, existe. Appelons-le x.
Soit y un nombre différent de x.
S’il est différent de x, c’est que |y – x| = d avec d > 0
Quel que soit d, il existe N tel que la largeur de IN soit inférieure à d.
y ne sera pas dans IN et ceci est vrai pour tout nombre y.
Seul x peut rester dans l’intersection des IN.
CQFD ?
Tu crées des problèmes là où il n'y en a pas. Ton raisonnement ci-dessus n'est pas "si x existe alors x existe"; c'est plutôt :Vanleers a écrit:Je crains que non et que l’on ait le raisonnement suivant : si x existe alors x existe.
Perplexité.
- x est dans l'intersection des IN (c'est un fait, les IN sont construits pour ça).
- Si y est différent de x, alors y n'est pas dans l'intersection des IN.
- Donc x est le seul élément dans l'intersection des IN.
Leonhard- Digressi(f/ve)

- Nombre de messages : 194
Date d'inscription : 03/09/2007
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Question très compliquée :)quid a écrit:C'est quoi un nombre réel ?
(Je sais, c'est trivial)
Complètement. Dans notre réalité physique, les seuls nombres ayant vraiment un sens sont les nombres décimaux (c.-à-d. ayant une écriture décimale finie) supérieurs à la plus petite grandeur physique possible (la longueur de Planck et ce genre de trucs), et inférieure à la plus grande grandeur physique possible (le nombre d'atomes dans l'univers et ce genre de trucs). Un rationnel comme 1/3 est déjà une abstraction !quid a écrit:C'est pour cela qu'un nombre réel est une abstraction.
Ça dépend de comment on définit les nombres réels. Si on les construit à partir des rationnels, alors on peut démontrer qu'ils forment un ensemble continue (ou "complet", dans le jargon).quid a écrit:Le fait que les nombres réels permettent de couvrir une continuité est en définitive plus un axiome que quelque chose qui se démontrerait. Les nombres réels sont introduits justement pour assurer la continuité numérique, pour traiter mathématiquement du continu.
Mais on pourrait alternativement déclarer qu'ils sont, par définition, un modèle de la "théorie des nombres réels", qui consiste en une liste d'axiomes; et là, la continuité (complétude) est effectivement un axiome :
https://fr.wikipedia.org/wiki/Nombre_r%C3%A9el#Approche_axiomatique
Leonhard- Digressi(f/ve)

- Nombre de messages : 194
Date d'inscription : 03/09/2007
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Toutes tes réflexions peuvent être appliquées au nombre 1/3.Magni a écrit:Vous faites comment pour donner une valeur de x ?
Vous dites que calculer ses décimales n'est qu'une façon d'appréhender x, vous avez quoi comme autre façon ?
Personne n'a jamais écrit, ni calculé effectivement toutes les décimales de 1/3. Comment peut-on appréhender autrement 1/3 que par son écriture décimale ? Réponse : par l'écriture "1/3", justement. Il s'agit d'une expression algébrique de longueur finie, pour laquelle on a développé de nombreuses règles de manipulation (le calcul des fractions). Depuis lors, on travaille avec cette écriture plutôt que l'écriture décimale.
Même chose pour pi. On peut appréhender pi par autre chose que son écriture décimale : par exemple, par son expression sous la forme d'une série (formule de Leibniz), mais aussi une intégrale, une limite, etc. Toutes ces formules ne sont que des écritures alternatives pour les nombres, et nous avons développé des règles de manipulation nous permettant de travailler avec ces écritures sans subir les limitations de l'écriture décimale (qui est pourrie). Ce qu'on appelle le calcul intégral, le calcul différentiel, le calcul des limites, c'est exactement ça. Et dans beaucoup de cas, toutes ces écritures non décimales des nombres en disent plus sur eux que leur écriture décimale.
Regardez comment on définit le nombre e, par exemple :
https://fr.wikipedia.org/wiki/E_(nombre)
En fait, il faut abandonner l'idée que l'écriture décimale d'un nombre est sa "véritable" apparence. L'écriture décimale n'est qu'une écriture culturellement arbitraire et remplie d'incommodités. Les maths consistent notamment à développer d'autres écritures, meilleures, des nombres.
Leonhard- Digressi(f/ve)

- Nombre de messages : 194
Date d'inscription : 03/09/2007
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
C'est hks qui surligne :
Outre le fait que relire Leibniz dans la lettre est toujours un grand plaisir, c'est l'une des plus belles proses françaises du XVII°. Tu as surligné " comme des fictions ", j'aurais surligné " choses idéales ", c'est la problématique du Sophiste de Platon et même Sade relève que " même des apparences, des fantômes, c'est des réalités ". Même un simple segment tracé est une tentative de représentation d'une chose idéale, de même pour la mesure, problème rappelé par Magni, qui demeure incomplète, inachevable, infiniment perfectible. Tu parles de " degré de réalité ", in fine la problématique vaut pour tout discours : je postule que pour chacun d'entre eux, on trouve en deçà, comme un substrat sine qua non, " l'infini qui se marre bien ". Pour les formalisations, les verbalisations, les discours, il est toujours déjà là, latent, et tout " discoureur " qui insiste, creuse, un peu finit par s'y heurter. Je suis vraiment désolé, je n'ai pas d'atomes crochus, a priori, etc., pour les mathématiques, mais force est de constater que c'est le discours qui s'en sort le mieux avec cet " animal rétif ", et ça, ça m'intéresse, j'espère quelque chose d'édifiant pour les autres discours avec l'infini, et donc à ce titre, même leurs difficultés, rappelées par Leonhard, m'intéressent.
hks a écrit:Il s'agit du degré de réalité des infiniment petits.Leibniz a écrit:je ne suis pas trop persuadé moy même, qu’il faut considérer nos infinis et infiniment petits autrement que comme des choses idéales ou comme des fictions bien fondées.
Outre le fait que relire Leibniz dans la lettre est toujours un grand plaisir, c'est l'une des plus belles proses françaises du XVII°. Tu as surligné " comme des fictions ", j'aurais surligné " choses idéales ", c'est la problématique du Sophiste de Platon et même Sade relève que " même des apparences, des fantômes, c'est des réalités ". Même un simple segment tracé est une tentative de représentation d'une chose idéale, de même pour la mesure, problème rappelé par Magni, qui demeure incomplète, inachevable, infiniment perfectible. Tu parles de " degré de réalité ", in fine la problématique vaut pour tout discours : je postule que pour chacun d'entre eux, on trouve en deçà, comme un substrat sine qua non, " l'infini qui se marre bien ". Pour les formalisations, les verbalisations, les discours, il est toujours déjà là, latent, et tout " discoureur " qui insiste, creuse, un peu finit par s'y heurter. Je suis vraiment désolé, je n'ai pas d'atomes crochus, a priori, etc., pour les mathématiques, mais force est de constater que c'est le discours qui s'en sort le mieux avec cet " animal rétif ", et ça, ça m'intéresse, j'espère quelque chose d'édifiant pour les autres discours avec l'infini, et donc à ce titre, même leurs difficultés, rappelées par Leonhard, m'intéressent.
_________________
" Tout Étant produit par moi m'est donné (c'est son statut philosophique), a priori, et il est Mien (cogito, conscience de Soi, libéré du Poêle) ". " Savoir guérit, forge. Et détruit tout ce qui doit l'être ", ou, équivalents, " Tout l'Inadvertancier constitutif doit disparaître ", " Le progrès, c'est la liquidation du Sujet empirique, notoirement névrotique, par la connaissance ". " Il faut régresser et recommencer, en conscience ". Moi.
C'est à pas de colombes que les Déesses s'avancent.

neopilina- Digressi(f/ve)

- Nombre de messages : 8364
Date d'inscription : 31/10/2009
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Je ne vois pas de discours.neopilina a écrit:mais force est de constater que c'est le discours qui s'en sort le mieux avec cet " animal rétif ",
De plus, serait- ce un discours, il ne traite pas de l'infini mais du dénombrable.(ou de l'indénombrable ... enfin bref du nombre)
Pour moi le degré de réalité d'un segment tracé n'est déjà pas le même que celui d'un segment pensé, a fortiori que d'un segment divisible en partie.
Plus c'est abstrait, est ce qu'on se rapproche ou est- ce qu'on s 'éloigne du réel ?
Eprouver le monde est tout à fait absent des mathématiques.
Elle sen glorifie d'ailleurs.
Pire, ses processus d'abstraction éloignent même du réel de la pensée.
hks- Digressi(f/ve)

- Nombre de messages : 12518
Localisation : Hauts de Seine
Date d'inscription : 04/10/2007
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
quid a écrit: C'est quoi un nombre réel ?
Un nombre complexe est un nombre à deux dimensions, une partie réelle et une partie complexe. Tout nombre complexe avec une partie complexe nulle est un nombre réel.
J'aime me représenter le complexe comme un nombre surfacique et le réel comme un nombre linéaire.
Dans les réels il y a un premier groupe avec les entiers positifs, l'entier nul, les entiers négatifs, les décimaux avec un développement décimal raisonnable et un deuxième groupe avec le reste : les décimaux avec un développement décimal déraisonnable, les rationnels, les algébriques non rationnels, et les transcendants (qui sont par définition non algébriques).
Un nombre décimal avec développement décimal non raisonnable c'est par exemple : trois virgule (les 31x10^12 première décimales de Pi). Si quelqu'un arrive à l'appréhender celui là je serais curieux de savoir comment et c'est infiniment moins compliqué à appréhender qu'un nombre transcendant, c'est seulement un nombre décimal à développement décimal fini.
On a eu besoin des entiers relatifs et des rationnels pour réussir à faire de la comptabilité.
Il faut les algébriques et les transcendants pour faire de la géométrie.
L'hypoténuse d'un carré de coté 1 est 2^0.5 (racine de 2)
(racine de 2) n'est pas un rationnel, il parait qu'un disciple de Pythagore est mort de n'avoir pas su garder cette information secrète, a l'époque on le savait déjà mais il n'était pas bien vu de le faire savoir pari les non initiés.
Pi n'est pas constructible, ce qui le rend non algébrique, on a besoin des transcendants pour ce type de nombre.
La nature des différents types de réels est liée aux caractéristiques des rapports de dimensions entre les éléments géométriques d'un espace euclidien. On a besoin de tous les types de réels en architecture.
On a aussi besoin des complexes en électricité.
On peut arbitrairement décider que le rapport entre le périmètre et le diamètre d'un cercle soit autre chose que Pi et on obtient des espaces courbes, non euclidiens.
Pi n'a la valeur usuel en géométrie que parce qu'on a décidé que les parallèles ne se rencontrent jamais.
Pi a la même valeur en physique parce qu'on considère que est dans un espace plat (de courbure nulle).
Mais certainement que l'espace de courbure nulle est plus naturel que les autres car on peut trouver Pi dans des formules numériques pure et élégantes comme la formule de Leibniz ou celle d'Euler.
_________________
Ce que je dis n'engage que moi.

Magni- Digressi(f/ve)

- Nombre de messages : 1065
Localisation : 62100
Date d'inscription : 03/05/2016
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
On ne sait pas appréhender les nombres non rationnels dans l'absolu, on ne sait que les appréhender approximativement, c'est à dire qu'on ne sait pas les appréhender.
On ne sait que les approcher avec des nombres décimaux à développement décimal raisonnable.
Le fait de faire une équations numérique n'est pas un raffinement révolutionnaire par rapport à faire une équation géométrique.
Les formules d'Euler ou de Leibniz ne donnent pas mieux Pi que définir Pi comme le rapport du périmètre au diamètre d'un cercle (dans un espace euclidien).
On ne sait que les approcher avec des nombres décimaux à développement décimal raisonnable.
Le fait de faire une équations numérique n'est pas un raffinement révolutionnaire par rapport à faire une équation géométrique.
Les formules d'Euler ou de Leibniz ne donnent pas mieux Pi que définir Pi comme le rapport du périmètre au diamètre d'un cercle (dans un espace euclidien).
_________________
Ce que je dis n'engage que moi.

Magni- Digressi(f/ve)

- Nombre de messages : 1065
Localisation : 62100
Date d'inscription : 03/05/2016
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Leonhard a écrit:En fait, il faut abandonner l'idée que l'écriture décimale d'un nombre est sa "véritable" apparence. L'écriture décimale n'est qu'une écriture culturellement arbitraire et remplie d'incommodités. Les maths consistent notamment à développer d'autres écritures, meilleures, des nombres.
Il faut abandonner l'idée que l'écriture décimale (avec un nombre de décimales raisonnable et fini) d'un nombre transcendant soit autre chose que la SEULE apparence qu'il offre à notre conscience.
Et oui, cette apparence de donne pas la "véritable" nature de ces nombres.
Vous vous trompez en disant que c'est incommode, on utilise des décimaux pour remplacer des transcendants alors que c'est inexacte mathématiquement parce que justement, c'est commode.
Il n'y a pas de meilleure façon d'écrire Pi que de dire que c'est le rapport du périmètre au diamètre d'un cercle (le formule d'Euler ne donne pas un meilleur Pi que ce rapport de dimensions géométriques).
On utilise quand même 3.14 à la place, parce que c'est utilisable, la phrase " le rapport du périmètre au diamètre d'un cercle" ou la formule d'Euler n'ont pas de résultat accessible mathématiquement et on ne les utilise pas en physique.
En physique, au moment de calculer un résultat numérique, on n'utilise les 15 premiers chiffres significatifs de Pi, on n'utilise pas Pi.
Partout ou on a vraiment besoin d'un résultat numérique et que Pi est un facteur non réductible, on n'utilise rien d'autre qu'une valeur approchée de Pi, pas parce que ça permet d'avoir un résultat erroné, ce n'est pas ça le but, mais parce que c'est la seule façon d'avoir un résultat, même si ça n'est pas un résultat tout à fait exact.
_________________
Ce que je dis n'engage que moi.

Magni- Digressi(f/ve)

- Nombre de messages : 1065
Localisation : 62100
Date d'inscription : 03/05/2016
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
hks a écrit:Je ne vois pas de discours.neopilina a écrit: .. mais force est de constater que c'est le discours [les mathématiques] qui s'en sort le mieux avec cet " animal rétif ", ...
C'est une formalisation, une " verbalisation ", même faite de signes, de symboles, etc., il y a des mots, les mathématiques sont une verbalisation, même une esthétique, c'est un " discours ", un Logos, même le " discours " très dérangeant, déconcertant, de l'aliéné est un discours profondément déterminé, fut-ce par de graves désordres, etc., encore faut-il, comme pour les mathématiques et autres, etc., être un initié aux ressorts du dit discours pour y entendre quelque chose. Les mathématiques sont pleinement, philosophiquement dit, une forme de discours, un Logos, et elles sont réputées pour être le plus rigoureux, même si bien sûr on ne peut pas leur demander de faire autre chose.
hks a écrit:De plus, serait-ce un discours, il ne traite pas de l'infini mais du dénombrable (ou de l'indénombrable, enfin bref du nombre).
Les camarades matheux sont plus compétents que moi pour réagir ici (et cela m'intéresse).
hks a écrit:Pour moi le degré de réalité d'un segment tracé n'est déjà pas le même que celui d'un segment pensé, a fortiori que d'un segment divisible en partie.
Plus c'est abstrait, est ce qu'on se rapproche ou est-ce qu'on s'éloigne du réel ?
Suis-je bien certain que ma représentation d'une fraise est plus tangible que ma représentation d'un segment tracé ? Non. Mais j'entends ton propos : le segment tracé ne sera jamais le segment pensé.
hks a écrit:Eprouver le monde est tout à fait absent des mathématiques.
Elles s'en glorifient d'ailleurs.
Pire, ses processus d'abstraction éloignent même du réel de la pensée.
Il faut distinguer le mathématicien qui fait des mathématiques pour faire des mathématiques, et d'autres, ingénieurs, mécaniciens, physiciens, etc., qui en font usage, avec une réussite sans pareille, pour étudier et décrire le réel, parfois au sens le plus radical qui soit. Le mathématicien s'arrange de l'infini comme il peut, et il sait bien, même s'il éprouve des difficultés avec, qu'il fait " partie des meubles ", a contario, les physiciens en ont une sainte horreur : par expérience, ils savent que quand l'infini, s'invite, s'impose, dans des calculs, des équations, des modélisations, etc., que ça va se terminer rapidement en grand n'importe quoi (sauf erreur, Leonhard rapporte que cela peut arriver aussi en mathématiques).
Bien sûr, le mathématicien peut nous apparaître bien " perché ", si j'ose dire, mais des philosophes occidentaux bien " perchés " (c'est à dire détacher du réel), j'en ai également vu pas mal, pour euphémiser, beaucoup trop à mon gout. Je comprends bien que le mathématicien puisse l'être, je le regrette quand c'est un philosophe. Et suite au cogito en l'état, on s'est retrouvé avec une philosophie occidentale académique philosophiquement carrément " stratosphérique ", coincée (par cette formulation du " Discours ") " en orbite ". En finance on parle de " bulle ", de même pour moi ici, rien de moins que la plus importante, prodigieuse et consternante de l'histoire de la philosophie occidentale. La philosophie l'a payé très cher et on est loin d'en être revenu.
De l'infini comme " substrat " ai-je dit. Pour moi, le concept du philosophe ou encore le 1, l'unité des mathématiques (je ne parle même pas d'un objet tel que pi donc), etc., etc., etc., en un mot, tout Etant généré par un être vivant a des racines qui plongent profondément dans l'infini. La physique nous dit que le réel est continu, c'est affaire de sciences naturelles, mais philosophiquement, je dis que la pensée l'est aussi mais que le substrat de celle-ci est l'infini ontologique et potentiel, c'est à dire l'Être.
Dernière édition par neopilina le Mer 21 Avr 2021 - 16:50, édité 3 fois
_________________
" Tout Étant produit par moi m'est donné (c'est son statut philosophique), a priori, et il est Mien (cogito, conscience de Soi, libéré du Poêle) ". " Savoir guérit, forge. Et détruit tout ce qui doit l'être ", ou, équivalents, " Tout l'Inadvertancier constitutif doit disparaître ", " Le progrès, c'est la liquidation du Sujet empirique, notoirement névrotique, par la connaissance ". " Il faut régresser et recommencer, en conscience ". Moi.
C'est à pas de colombes que les Déesses s'avancent.

neopilina- Digressi(f/ve)

- Nombre de messages : 8364
Date d'inscription : 31/10/2009
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
hks a écrit:
Plus c'est abstrait, est ce qu'on se rapproche ou est- ce qu'on s 'éloigne du réel ?
Eprouver le monde est tout à fait absent des mathématiques.
Elle sen glorifie d'ailleurs.
Pire, ses processus d'abstraction éloignent même du réel de la pensée.
Plus c'est métaphysique et plus c'est "au delà" du monde physique.
Moins physique ne veut pas dire moins réel, cela ne veut pas dire non plus moins irréel.
Si on parle de Pi qui est une concept métaphysique inaccessible dans le monde physique, plus on s'éloigne du tangible et qu'on va dans l'abstraction et plus on approche la réalité de Pi.
Pour tout ce qui est sensible, accessible à travers nos sens physiques, le fait de ne pas pratiquer l'abstraction est possible pendant qu'on est en train de ressentir, mais comment ne pas perdre complètement la réalité du moment quand le moment est passé si on ne pratique pas l'abstraction ?
Qu'est qui est réel pour toi ?
La table de ta cuisine est elle toujours réelle pour toi quand tu n'es pas dans ta cuisine en contact physique avec la réalité de la table.
Si oui, comment ta table de cuisine peut elle être toujours réelle pour toi quand tu n'es pas dans ta cuisine sinon à travers l'accessibilité mentale à une abstraction métaphysique de ta table ?
Quand tu n'es pas en contact physique avec ta table, ton processus d'abstraction de la table te rapproche de la réalité de cet objet.
Si tu ne pratiques pas l'abstraction, ta table disparaît totalement de ta réalité quand elle n'est pas en ta présence directe.
_________________
Ce que je dis n'engage que moi.

Magni- Digressi(f/ve)

- Nombre de messages : 1065
Localisation : 62100
Date d'inscription : 03/05/2016
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
hks a écrit:De plus, serait-ce un discours, il ne traite pas de l'infini mais du dénombrable (ou de l'indénombrable, enfin bref du nombre).
Le dénombrable se représente avec des nombres.
Le non dénombrable se représente avec des infinis, les infinis ne sont pas des nombres, le non dénombrable se manipule avec des non-nombres.
neopilina a écrit:La physique nous dit que le réel est continu, c'est affaire de sciences naturelles, mais philosophiquement, je dis que la pensée l'est aussi mais que le substrat de celle-ci est l'infini ontologique et potentiel, c'est à dire l'Être.
La physique ne nous dit pas que le monde physique est continu.
La mécanique relativiste abandonne toute prédiction avant d'arriver au continu.
Pour tout ce qui se passe dans un temps plus court que le temps de Planck ou dans un espace plus petit que la longueur de Planck, la mécanique relativiste déclare forfait.
Quant à la mécanique quantique, elle est établit sur la théorie des quantas et ne considère rien de continu dans le monde physique.
L'intuition nous donne une approche du monde physique qui visualise le continu, mais l'intuition est une abstraction de la réalité physique.
_________________
Ce que je dis n'engage que moi.

Magni- Digressi(f/ve)

- Nombre de messages : 1065
Localisation : 62100
Date d'inscription : 03/05/2016
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Je souhaite pas répondre à toutes tes observations (sensées mais peut -être trop parallèles au sujet)Magni a écrit:mais comment ne pas perdre complètement la réalité du moment quand le moment est passé si on ne pratique pas l'abstraction ?
Ce qui se réfère à la mémoire . Est- t elle abstractive ? La recherche du temps perdu (Proust) est -ce une abstraction ?Magni a écrit:mais comment ne pas perdre complètement la réalité du moment quand le moment est passé si on ne pratique pas l'abstraction ?
Pour moi la réalité de mon bureau /table est certainement plus dans la mémoire que j'en ai que dans l'abstraction délivrée par la physique.
hks- Digressi(f/ve)

- Nombre de messages : 12518
Localisation : Hauts de Seine
Date d'inscription : 04/10/2007
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
On peut même dire que les mathématiques constituent un archétype du discours pur solipsiste, c'est-à-dire du langage qui, par nature, ne parle que de lui-même. Le prix à payer pour atteindre la cohérence absolue est bel et bien le renfermement sur soi. (Est-ce la raison pour laquelle des logiciens frôlent la folie ?) Les mathématiques ne parlent pas du monde réel; ce dont elles parlent est d'ailleurs une question ouverte en philosophie des mathématiques. Mais en première approximation, on peut dire qu'elles parlent de concepts formels, en les analysant, tissant des liens entre eux, etc.neopilina a écrit:Les mathématiques sont pleinement, philosophiquement dit, une forme de discours, un Logos, et elles sont réputées pour être le plus rigoureux, même si bien sûr on ne peut pas leur demander de faire autre chose.
L'infini également est une idée, un concept, et non une chose de notre réalité concrète. On admet communément que l'infini ne fait pas partie de notre monde.
Ce n'est donc pas étonnant qu'un discours ayant notablement donné de la texture aux idées d'infini soit le discours mathématique. Les deux sont hors du monde. Car les aspects de l'infini sont nombreux en mathématiques : on en trouve dans le domaine des nombres, mais également celui des ensembles, de la géométrie ou même de la logique.
Pensons par exemple à la géométrie projective qui est une géométrie fondée sur l'axiome que "deux droites se croisent toujours en un point", avec l'idée que si l'on a deux droites parallèles, alors elles se croisent en un point "à l'infini". Pensons aussi aux logiques dites "infinitaires", dans lesquelles on peut, à partir d'une infinité d'énoncés P1, P2, ..., former la conjonction infinie "P1 et P2 et ...", ainsi que la disjonction infinie "P1 ou P2 ou ...".
https://fr.wikipedia.org/wiki/Logique_infinitaire
Le niveau de détail et la richesse des déclinaisons sémantiques que les mathématiques ont apporté à l'idée d'infini sont remarquables.
Pendant que certains sont bloqués, par principe métaphysique, face à l'idée d'infini, les mathématiciens, eux, jouent avec sans trop se poser de questions existentielles.
Leonhard- Digressi(f/ve)

- Nombre de messages : 194
Date d'inscription : 03/09/2007
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
hks a écrit:Ce qui se réfère à la mémoire . Est- t elle abstractive ? La recherche du temps perdu (Proust) est -ce une abstraction ?
Pour moi la réalité de mon bureau /table est certainement plus dans la mémoire que j'en ai que dans l'abstraction délivrée par la physique.
Ce n'est pas réellement ta table de cuisine qui est dans ton cerveau.
Je crois que ta table de cuisine est bien plus réellement dans ta cuisine que dans ta tète.
Tu es libre de croire ce que tu veux.
Dernière édition par Magni le Jeu 22 Avr 2021 - 9:53, édité 1 fois
_________________
Ce que je dis n'engage que moi.

Magni- Digressi(f/ve)

- Nombre de messages : 1065
Localisation : 62100
Date d'inscription : 03/05/2016
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Tu me parles du moment (instant présent )magni a écrit:mais comment ne pas perdre complètement la réalité du moment quand le moment est passé si on ne pratique pas l'abstraction ?
Si je ne perds pas la réalité tout court celle du moment y compris, c'est plus parce que j'ai de la mémoire que parce que j'ai une faculté d abstraction.
C'est tout ce que je disais .
Et cecl n'est pas du tout une réponse à la question : où est la réalité de la table ?
.......................................................
Problème de la liberté après celui de la mémoire )magni a écrit:Tu es libre de croire ce que tu veux.
Je ne me sens pas libre du tout, de croire ce que je veux.

Dernière édition par hks le Jeu 22 Avr 2021 - 15:38, édité 1 fois
hks- Digressi(f/ve)

- Nombre de messages : 12518
Localisation : Hauts de Seine
Date d'inscription : 04/10/2007
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?

à neopilina
Difficile pour moi de se sortir du piège: "degré" de réalité car il laisse supposer une hiérarchie en qualité.(ou perfection)
je disais simplement que les tiges de bois (qui sont des
proto segments ) ne sont pas de la même réalité que le segment pensé par la géométrie lui même pas encore de la même réalité que le segment gradué.
.......................................................................................................
Sur le continu
désolé de penser comme Spinoza (il faut maintenant s'en excuser)
scolie prop 15 partie 1Spinoza a écrit:Et si cependant on demande maintenant pourquoi nous avons, de nature, un tel penchant à diviser la quantité ? je réponds que nous concevons la quantité de deux manières abstraitement, autrement dit superficiellement, dans la mesure où nous l'imaginons, ou bien comme substance, ce qui se fait par le seul intellect. Si donc nous prêtons attention à la quantité telle qu'elle est dans l'imagination, ce que nous faisons souvent et avec plus de facilité, on la trouvera finie, divisible, et composée de parties; et, si nous lui prêtons attention telle qu'elle est dans l'intellect, et la concevons en tant qu'elle est substance, ce qui se fait très difficilement, alors, comme nous l'avons suffisamment démontré, on la trouvera infinie, unique, et indivisible. Et cela, tous ceux qui auront su faire la distinction entre l'imagination et l'intellect le trouveront assez manifeste : surtout si l'on prête également attention à ceci, que la matière est partout la même, et qu'on n'y distingue de parties qu'à la condition de la concevoir, en tant que matière, affectée de manières diverses, si bien que ses parties ne se distinguent que par la manière, et non en réalité. Par ex., l'eau, en tant qu'elle est eau, nous concevons qu'elle se divise, et que ses parties se séparent les unes des autres; mais pas en tant qu'elle est substance corporelle; car en tant que telle elle ne se sépare ni ne se divise.....(le texte est beaucoup plus long)
http://ethicadb.org/pars.php?parid=1&lanid=0&lg=fr
Et je n'ai pas envi d'en discuter plus avant sur ce fil.
Dernière édition par hks le Jeu 22 Avr 2021 - 15:38, édité 1 fois
hks- Digressi(f/ve)

- Nombre de messages : 12518
Localisation : Hauts de Seine
Date d'inscription : 04/10/2007
Page 6 sur 9 •  1, 2, 3, 4, 5, 6, 7, 8, 9
1, 2, 3, 4, 5, 6, 7, 8, 9 
Page 6 sur 9
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum

 par hks Mar 20 Avr 2021 - 21:54
par hks Mar 20 Avr 2021 - 21:54