Re: L'infini est-il limité ?

[Magni]

Vous déplorez donc qu'on ne puisse mesurer à l'aide de règles graduées et donc construire la diagonale dans l'espace matériel alors qu'elle y est bel et bien tracée .

Je ne déplore rien du tout.

Quand je trace l'hypoténuse d'un triangle rectangle isocèle, je fais une représentation graphique de la racine carré de la longueur des cotés droits.
Le triangle tracé est physique, avec ses défauts et ses imperfections, et il représente un triangle métaphysique, sans défaut ni imperfection.

Tout ce qui est constructible géométriquement est algébrique, donc je n'ai pas besoin de mesurer racine de 2, je peux le calculer avec une précision suffisante pour n'importe quel usage.

Peut être vivons nous tous les deux dans deux réalités différentes.




En mathématique, rationnel signifie que ce n'est pas irrationnel.
Dire que les nombres irrationnels sont rationnels ça porte à la confusion, vous devriez choisir un autre terme, "logique" par exemple. Racine de 2 est un nombre obtenu de façon tout à fait logique à partir d'une construction géométrique ou à partir d'un polynôme à coefficient entiers.

[neopilina]

Ontologiquement le tracé matériel échappe à la mesure.

Surtout pas " ontologiquement ". Dans certains ateliers, industries, laboratoires, etc., on fixe une exigence de précision, j'ai par exemple vu une installation où la précision exigée était le micron. Pour ce qu'on y faisait, le micron c'était bien, parfait, suffisant, etc. Il y a d'autres domaines où on exigera une précision encore plus grande dans la mesure physique, potentiellement infiniment perfectible, c'est tout (sauf erreur de ma part, aujourd'hui on peut mesurer à l'atome près, là où on en a besoin). Là, on parle juste des moyens techniques, des outils, dont nous, nous disposons. C'est très concret, pas d'ontologie, pas de philosophie, de métaphysique, etc., ici. De la physique. Par nature, définition, les métaux présente une structure atomique cristalline, c'est à à dire qu'il y a une organisation géométrique des atomes, et bien cela s'observe et se mesure.

[Leonhard]

Je suppose qu'il ne vaut mieux pas faire intervenir la physique quantique et le fait qu'au niveau fondamental de la matière, le résultat d'une mesure est aléatoire...

[neopilina]

Je suppose qu'il ne vaut mieux pas faire intervenir la physique quantique et le fait qu'au niveau fondamental de la matière, le résultat d'une mesure est aléatoire...

Tout à fait ! Mais pour la " très étrange ", de notre point de vue, physique quantique, je serais aux abonnés absents !

[hks]

à Magni

Certes "déplorer" est sans doute excessif dans ton cas puisque tu divises en physique et métaphysique.
la question de l'adéquation ne se pose pas cruellement.

je divise moi aussi mais entre un accès perceptif (ou disons sensible) et le cognitif.
Je ne fais pas du cognitif (dont la rationalité mathématique) quelque chose de métaphysique.

Dire que les nombres irrationnels sont rationnels

j'ai dit fondée sur une rationalité systématique.

parce que je pense les mathématiques comme une cognition systématique et logique qui a construit les irrationnels (et les a construit rationnellement)

En mathématique, rationnel signifie que ce n'est pas irrationnel.

je ne parle pas en langage mathématique ou avec son lexique . Je te parle en langage ordinaire.
Et en langage ordinaire on peut dire qu'il est rationnel de poser comme sujet d'étude ou de formalisation : les nombres irrationnels.

[hks]

Surtout pas " ontologiquement ". Dans certains ateliers, industries, laboratoires, etc., on fixe une exigence de précision, j'ai par exemple vu une installation où la précision exigée était le micron.

tu abondes dans mon sens sans le vouloir.
Avant l'exigence de mesure... il est quoi "ontologiquement"
l'objet ?
Si avant l'exigence de mesure, il n'est rien ontologiquement... il faut le dire ( ce serait un scoop chez toi)

[neopilina]

Surtout pas " ontologiquement ". Dans certains ateliers, industries, laboratoires, etc., on fixe une exigence de précision, j'ai par exemple vu une installation où la précision exigée était le micron.

tu abondes dans mon sens sans le vouloir.
Avant l'exigence de mesure... il est quoi "ontologiquement"
l'objet ?
Si avant l'exigence de mesure, il n'est rien ontologiquement... il faut le dire   ( ce serait un scoop chez toi)

Envie de jouer !? Il va bien sûr de soi que toute chose est d'abord, pour moi, un Etant (Mien), i.e., pléonasme, ontologiquement dit. " Ensuite ", il y a, au cas échéant, le besoin, l'envie, la nécessité, etc., d'une mesure, au degré de précision souhaité, de telle ou telle chose. Tu as posté une photographie de grumes de bois, honnêtement, je n'ai pas trop compris. Mais à ce niveau, on ne s'encombre pas du centimètre (en fait pour le bois, la mesure usagée est le mètre cube avec une décimale, le stère).

[Magni]

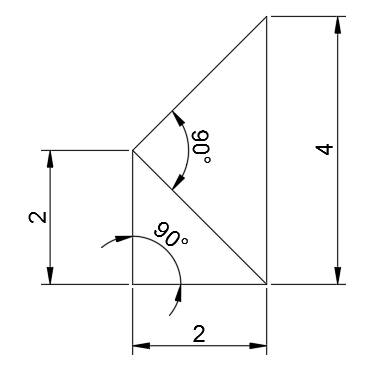
J'ai fais ce croquis sur Autocad, c'est un logiciel de dessin "vectoriel", ce qui signifie que le tracé est en acte parfaitement géométrique.

Toute géométrie étant algébrique, la puissance de nos machines de calcul nous permettent maintenant de ne plus faire d'imperfections dans le tracé en basant le tracé sur le calcul et non l'inverse.
Ici, le tracé EST un calcul, et il a la précision du calcul.


Bien évidemment, si on imprime sur papier ou en 3D, et qu'on mesure, on retrouve l'imprécision de la mesure.

[neopilina]

Bien évidemment, si on imprime sur papier ou en 3D, et qu'on mesure, on retrouve l'imprécision de la mesure.

Bien sûr. Vous, je sais pas, mais moi, dés le CM2, l'exercice de T.P. qui nous permettaient de retrouver par nous mêmes Pi, le cercle tracé par le compas m'a plongé dans une perplexité insondable !!  

Mettez vous un instant à la place du fabricant des roulements à billes qui vont pulluler dans une fusée. Le dernier problème, chronique, rencontré par Von Braun avec ces V2 était un problème de gyroscope. Quand on lui a annoncé qu'enfin un V2 avait atteint sa cible, il a eu cette étrange réaction : " Pour la première fois dans l'histoire une fusée a atteint sa cible, mais ce n'était pas sur la bonne planète ". Est-ce que les succès de ses lanceurs pour la N.A.S.A l'ont aidé à oublier les victimes de ses premiers engins ? Je ne sais pas, il n'y a que lui qui l'a su.

[rentan]

Pour moi, l'Univers est comparable à la pensée. Est-ce que l'on peut affirmer que la pensée humaine est finie ? Oui pour des raisons biologiques si l'être qui l'utilise disparaît mais tant que cet être existe, il peut penser de manière infinie. J'ai l'intuition que l'Univers fonctionne comme une pensée.

[hks]

Tu as posté une photographie de grumes de bois, honnêtement, je n'ai pas trop compris.

Tu poses une grume, tu construis un carré  autour de la grume/bâton tel que  ce bâton en soit la diagonale .
Tu as un bâton qui mesure:  coté du carré X racine de 2
Comme dirait Magni ce n'est pas une mesure exacte. C'est une mesure  infinie.
Le bâton fini qui sert de diagonale est- il limité ?
le fini est- il limité?

Hors d'un certain nombre de précautions est- ce que la question a du sens ?
Et je dis que les questions de Leohard demandent un certain nombre de précautions.

Le fini est- il limité?
savoir dans quel contexte on pose les questions.

[Magni]

Pour moi, l'Univers est comparable à la pensée. Est-ce que l'on peut affirmer que la pensée humaine est finie ? Oui pour des raisons biologiques si l'être qui l'utilise disparaît mais tant que cet être existe, il peut penser de manière infinie. J'ai l'intuition que l'Univers fonctionne comme une pensée.

On peut, sans preuve, affirmer ce qu'on veut; mais on ne peut pas prouver que la pensée humaine est finie.

Je crois que la pensée humaine est continue dans l'infiniment petit et présente dans l'infiniment grand. D'une façon holistique que je vois d'un oeil gnostique mais aussi de façon pratique et expérimentale. La pensée humaine transcende le temps, on peut reprendre ses pensées, les réorganiser, les arrêter pour penser à autre chose, les reprendre après les avoir interrompues.

Si vous interrompez le cours de ma réflexion, je pourrais toujours en reprendre le fil là où il avait été sectionné et faire que ma réflexion elle-même soit continue.
Si l'idée que je veux bâtir utilise des concepts trop ambitieux pour la capacité de refroidissement de mes neurones, je peux toujours prendre des notes et "prendre du temps" pour infuser les principes dans ma conscience avant de reprendre ma construction avec un peu plus de capacités intellectuelles.
L'interruption du cours de mes pensées ne brise pas ma réflexion.

Pour cela et pour d'autres raisons, la pensée humaine n'est pas causale, une des autres raisons étant que par nature, la pensée humaine est sa propre cause.
Peut-être pas pour les larves d'humain avant le stade de la conscience de soi, mais pour les humains suffisamment éveillés du bulbe cérébral pour savoir ce qu'est un sapiens et se reconnaître comme tel, la pensée du sujet à pour objet principal le sujet lui même. L'humain est soit égocentrique et se demande ce qu'il peut prendre dans le monde, ou alors il est altruiste et il se demande ce qu'il peut donner au monde, chacun étant un amalgame des deux, et dans les deux cas l'individu est le passage du sable de son sablier temporel personnel dans lequel il déroule des variations de scénarii potentiels pour choisir la voie de son destin avant d'emprunter la voie de la réalisation de ses ambitions avec des actes.
Même si nous ne pensons pas à toutes les variations possibles intermédiaires image par image, nous choisissons des intervalles bornés, et aussi longtemps que l'action ne dépasse pas les bornes de nos prévisions nous serons satisfaits d'avoir le sentiment de la réalisation de notre volonté. L'infini existe dans la somme de tous les possibles que nous sommes capables d'envisager.

Par contre, il ne faut pas tenter d'introduire cet infini dans les actions, pour se réaliser effectivement, l'action doit être mesurée.

[Magni]

Comme dirait Magni ce n'est pas une mesure exacte. C'est une mesure  infinie.

J'ai dis que la mesure n'est pas de précision infinie, justement parce que la mesure est physique et l'infini est au delà du monde physique, la mesure finie, limitée.

Platon : L'humain est la mesure de toute chose
Horace : Il faut de la mesure en toute chose
Max Planck : Il y a une limite physique à la précision de la mesure.

La mesure expérimentale et empirique n'est absolument pas infinie, elle est aléatoire.

Ce n'est pas parce que la suite aléatoire des décimales de Pi est infinie que tout ce qui est aléatoire est infini.
Et pour mémoire, l'aléatoire n'échappe pas au déterminisme, ça n'a rien à voir avec le hasard.
Jetez un dé, vous obtiendrez un tirage aléatoire fini, vous pouvez toujours croire que le mouvement de déplacement du dé fut continu avec une infinité de positions, voir avec une infinité de trajectoires et résultats possibles, peu importe, toutes ses positions et possibilités auront vite été épuisées par le destin du dé qui est de donner un tirage sans délai.

[Magni]

Connaissez vous Roland moreno ?, il est l'inventeur de la puce des cartes à puce.

dans son livre "la théorie du bordel ambiant", il explique comment fonctionne un générateur de nombres aléatoires informatique et comment il a réalisé un générateur d'aléatoire électronique.

La fonction "randominize" des logiciels exploitent des suites de décimales de nombres non algébriques. Le premier random de l'histoire informatique donnait la suite des chiffres de 2^(0,5) à partir de la millième décimale, gardant la position en mémoire de masse et incrémentant à chaque nouvelle commande random. Les paramètre initiaux ont évolué mais la méthode est toujours la même.

Monsieur Moreno a créer un "calculateur de hasard" autour d'une résistance (le mot "hasard" est ici une appellation comique, pas une prédiction scientifique). En mettant un peu plus de courant que la capacité de la résistance, celle si surchauffe un peu, et l'intensité monte vers un pic d'hystérésis chaotique, sensible à la température à tel point que le battement d'aile de papillon devient une cause effective. La mesure de l'intensité donne alors des résultat imprédictible et en choisissant bien le moment de la mesure et le traitement du signal, on obtient de l'imprédictible équipotentiellement réparti sur un segment de valeur divisibles par dix.

[jean tardieu]

, la pensée humaine est sa propre cause.

Là-dessus j'émettrais quelques réserves : la cause de la pensée humaine se constitue des émotions provoquées en réaction à des stimuli -externes - captés par les sens, ou - induits - provoqués par des émotions produites par le psychisme lui-même.
Le processus lui-même peut être considéré comme ininterrompu puisque le psychisme travaille h24, tout comme les autres organes, même dans le sommeil.

[Magni]

En linguistique, on dit que les phrases des langages humains ont une capacité de concaténation de l'information infinie.
La possibilité de conceptualiser une infinité de principes ne signifie pas qu'on a effectivement réalisé cette infinité.

Mais la pensée humaine n'a pas moins de capacité que le langage humain en tant que la pensée exploite le langage.

Ce n'est pas par mes seules capacités individuelles mais parce que je peux reprendre la pensée d'Aristote et la poursuivre que je dis que la pensée humaine touche au continu et à l'infini.

Le fait que nous sommes des être animés même pendant nos phases de sommeil est un passage ouvert vers une autre sorte d'infini.

[hks]

Si vous interrompez le cours de ma réflexion, je pourrais toujours en reprendre le fil là où il avait été sectionné et faire que ma réflexion elle-même soit continue.

c 'est la magnitude.

Magni attitude

passer outre les interruptions.

[quid]

Vos échanges m'empêchent de dormir.
Alors j'y vais de ma petite explication :
Les points mathématiques d'un segment sont virtuels, donc indéfinis donc infinis.
Il n'en va pas de même pour le physicien qui peut aligner des atomes, de dimensions connues, donc dénombrables (voir nombre d'Avogadro).
Pour le physicien, l'infini n'existe donc pas. Et la manoeuvre est tout à fait faisable : on dépose bien une couche de l'épaisseur d'un atome d'or sur un métal donné par électrolyse.
Quant à l'espace qui lie les atomes, il faut des énergies de l'ordre de 126 Gev pour le casser. De tels niveaux d'énergie pour "casser" du vide, c'est difficilement imaginable. Donc il n'y a pas de vide, donc l'espace est continu et dénombrable.
Idem pour le carré.
Idem pour l'univers.
Les mathématiciens jouent avec du virtuel, qui n'est même pas du potentiel. Infini.
Les physiciens jouent avec des noyaux et des photons, de la matière. Finie.

Moi j’ai toujours la même question : Et l’espace ? C’est de la matière ? C’est du vide ? Entre deux objets dans l’espace il y a quoi ? C’est discret ou continu ce qu’il y a ?
En termes de matière, imaginons que l’on arrive jusqu’à l’insécable. Si cet insécable c’est l’atome par exemple, tu dis bien qu’il a une épaisseur. Si l’on empile les atomes et bien la couche d’atomes ne fait pas la même épaisseur. Si l’insécable c’est le quantum (je parle toujours de matière et non pas de vide) même ce quantum a une « épaisseur » qui n’est pas rien, dont on évalue une valeur.
Imaginons que l’espace (donc y compris le vide) soit discret, un peu comme les pixels d’un écran, on pourrait nommer cette unité d’espace insécable le « spatium », une sorte de longueur de Planck. En termes d’occupation de l’espace, on aurait alors un quantum mesure « n » « spatia » avec n un entier et n >= 1. Mais on arrive à la même impasse : Si 2 « spatia » peuvent se juxtaposer et forment un espace plus grand, ils ont aussi une certaine dimension non nulle. Comme l'a dit neopilina en faisant référence à Aristote, où est alors le lieu du lieu, c’est-à-dire la dimension de l’insécable (qui n’est pas virtuelle pour le coup) ?

[quid]

Donc, dire qu'un nombre est défini par son développement décimal infini ne permet pas de définir un nombre transcendant dans le monde physique, ce nombre reste physiquement inaccessible.

Le caractère physiquement accessible ou pas d'un nombre n'a aucune influence sur sa définition mathématique.

Quand un nombre n'est pas constructible géométriquement et s'il est non algébrique, c'est un nombre transcendant.

Le fait qu'un nombre soit physiquement accessible est en relation avec le fait que ce nombre est constructible géométriquement, ce type de nombre est algébrique, selon la définition mathématique des nombres algébriques.

"racine carré de 2" est constructible, on peut physiquement le dessiner à la règle et au compas comme étant l'hypoténuse d'un carré de coté 2, il donc est algébrique, c'est la racine d'un polynôme à coefficient entier (x^2=2).

Pi ne peut pas être construit à la règle et au compas et il est non algébrique.

Il est physiquement impossible de tracer un segment qui mesure exactement la racine carrée de 2. L'épaisseur du trait et la texture du support introduisent déjà de l'imprécision, sans compter le fait qu'à l'échelle microscopique, la précision sera limitée par la discontinuité des mesures possibles.

Racine de 2, est hors de portée d'une construction physique. (Rappelons qu'il possède une infinité de décimales également.)

Les constructions dites "à la règle et au compas" de la géométrie antique sont déjà des idéalisations mathématiques.

On n'a pas plus la valeur numérique exacte de "racine de 2" que la valeur numérique exacte de Pi.

Je ne suis pas persuadé de cela
mais Leonhard en parlerait mieux que moi .

Magni a raison. Racine de 2, tout comme pi, sont des irrationnels, et leur développement décimal est illimité et non périodique. Pour connaître une décimale à une position donnée, il est donc nécessaire de la calculer explicitement, or il y en a une infinité...

Si l'on n'a pas la valeur numérique exacte de certains nombres, cela pose la question de ce qu'est un nombre, parce-que dans nombre, je lis "numérique".

En représentation décimale, un nombre peut avoir soit un nombre fini de décimales, soit un nombre infini (il peut aussi et théoriquement, en infiniment grand, avoir un nombre infini de chiffres pour sa partie entière) :

- Racine carrée de deux, c'est une notation non numérique, tout comme Pi. L'opérateur "racine carrée" n'est pas un opérateur trivial. Sa notation décimale comporte un nombre infini de décimales. Des formules de calcul à développement infini permettent de l'approcher.
- Pi a aussi un nombre de décimales infini, et il existe aussi une formule (formule de Leibniz) à développement infini qui permet de l'approcher. (on est dans le domaine des formules).
- 1/3 (un tier) a aussi un développement décimal à l'infini (0.33333...). Même si le chiffre décimal suivant est facile à anticiper (3), et ne nécessite pas de formule de calcul, on a la même problématique que pour Pi ou que racine de 2 quant à son écriture décimale qui demande un développement à l'infini.

Alors qu'est-ce que ces nombres, s'ils n'ont pas de représentation numérique ? La meilleure représentation qu'on puisse en faire est géométrique, mais on n'est plus vraiment dans le domaine du numérique. Cependant on a bien des lignes continues qui ont des longueurs différentes, et surtout qui entretiennent entre elles des rapports remarquables lorsqu'elles s'inscrivent dans certaines figures géométriques. Je parle bien sûr de figures géométriques idéales, parfaites, exactes, et donc de mesures et de rapports qui le sont également.

Si l'on peut tracer un segment de droite qui fait idéalement racine carrée de 2 ou encore 1/3, cela permet de mieux visualiser ces grandeurs, de les concrétiser en quelque sorte (même si l'on parle de figures géométriques idéales). Cependant, puis-je dire alors que j'ai obtenu ces nombres, leur représentation ?
Pour Pi, certes il n'est pas possible (a priori) de tracer idéalement un segment de droite de cette longueur. Cependant en traçant idéalement un cercle, j'ai bien ce nombre sous forme d'une ligne continue non droite. Pour tracer racine carré de 2 on doit passer par un plan en deux dimensions, il est impossible de le tracer directement sur un segment de droite, et bien pour Pi on doit passer par la ligne courbe. Au final, que cela soit sous forme d'une représentation par le segment de droite de la diagonale d'un carré, d'une représentation en trois segments égaux, ou par celle d'une représentation par un cercle pour Pi, on obtient bien un tracé fini qui dans chacun des cas n'est pas numérique.

Un nombre, c'est une double abstraction : Puisqu'il s'abstrait à la fois d'une forme numérique, et d'une dimension géométrique pratique (qui est donc de l'ordre de l'idéal)

[rentan]

Pour moi, l'Univers est comparable à la pensée. Est-ce que l'on peut affirmer que la pensée humaine est finie ? Oui pour des raisons biologiques si l'être qui l'utilise disparaît mais tant que cet être existe, il peut penser de manière infinie. J'ai l'intuition que l'Univers fonctionne comme une pensée.

On peut, sans preuve, affirmer ce qu'on veut; mais on ne peut pas prouver que la pensée humaine est finie.

Je crois que la pensée humaine est continue dans l'infiniment petit et présente dans l'infiniment grand. D'une façon holistique que je vois d'un oeil gnostique mais aussi de façon pratique et expérimentale. La pensée humaine transcende le temps, on peut reprendre ses pensées, les réorganiser, les arrêter pour penser à autre chose, les reprendre après les avoir interrompues.

Merci d'avoir répondu. Déjà, je pense que l'esprit humain (enfin, le mien...) n'est pas outillé pour réfléchir sur l'infinité, il faudrait lui enlever ses propres limites innées ou acquises. C'est pour cela que je parle d'intuition, car celle-ci est moins structurée que la réflexion. Elle fait appel à la pensée spontanée et non à des théories certes magnifiquement élaborées mais qui se heurtent à la triste réalité de la contradiction.

L'Univers que l'on essaie d'imaginer est peut-être effectivement fini et continué par un autre, un peu comme les lignes du carré qui figuraient dans la question d'origine de ce fil. Une superposition d'univers, maos du coup plutôt sphérique et non carrée parce que "qu'est-ce qu'il y a autour du carré?"

Penser à l'infiniment grand revient à essayer de combler le vide et penser à l'infiniment petit revient à creuser le plein. C'est vrai, l'infiniment petit, on sait ce qu'il y a autour alors que l'infiniment grand, on sait pas.

[hks]

Moi j’ai toujours la même question : Et l’espace ? C’est de la matière ? C’est du vide ? Entre deux objets dans l’espace il y a quoi ? C’est discret ou continu ce qu’il y a ?

Il y a pire comme question.

Entre deux espaces remplis celui de l'instant t1 et celui de l'instant t2... il y a quoi comme espace ?

[rentan]

Il y a l'espace d'un instant.

[hks]

l'espace d'un instant...  certes, un peu de poésie ne nuit pas.

mais un peu de réflexion non plus

C'est vrai, l'infiniment petit, on sait ce qu'il y a autour alors que l'infiniment grand, on sait pas.

L'infiniment petit, on sait ce qu'il y a autour...  c'est l'infiniment grand
l'infiniment grand, on sait ce qu'il y a dedans ...c'est l'infiniment petit.
Ce qu'on voit, c'est qu'on connait l'un par l'autre et inversement.

Si on pense l'espace comme absolu (sans rien de précis en lui) alors il persiste  sans  que les instants interviennent.
Le problème est qu'on a beaucoup de difficulté à penser un espace vide. A le "penser" encore passe, que ne pense-t on pas par abstraction !
 Mais à le sentir comme absolument vide, ça passe moins.

[quid]

Moi j’ai toujours la même question : Et l’espace ? C’est de la matière ? C’est du vide ? Entre deux objets dans l’espace il y a quoi ? C’est discret ou continu ce qu’il y a ?

Il y a pire comme question.

Entre deux espaces remplis celui de l'instant t1 et celui de l'instant t2... il y a quoi comme espace ?

Il y a l'espace d'un instant.

Oui, l'espace d'un instant. Effectivement la problématique se retrouve aussi dans le cinématique. Y a-t-il une durée insécable ("tempus"    ) ? Qui a cependant une durée non nulle, qui oblige l'écoulement.
Mais de manière générale, si l'on a du discret (matière, espace, temps) d'une certaine valeur non nulle, qu'est-ce qui cependant assure la transition entre les juxtapositions ? La continuité ne semble pas être une illusion comme les images d'un film, car pour qu'il y ait un film et non plus des images, il faut bien que les images s'agencent dans un "substrat" continu.

Les nombres ne sont-ils pas toujours, au départ, la valeur de quelque chose ? Ne sont-ils pas construits sur des notions intuitives ? Est-ce que ce qui fait la cohérence des mathématiques qui travaillent sur les nombres en tant que tels, ne relève pas tout de même de quelque chose auxquels ils s'appliquent ? Ce à quoi ils s'appliquent, le fondement de leur cohérence n'est-il pas le géométrique justement ?

[Magni]

Alors qu'Est-ce que ces nombres, s'ils n'ont pas de représentation numérique ? La meilleure représentation qu'on puisse en faire est géométrique, mais on n'est plus vraiment dans le domaine du numérique.

J'aimerais bien mais non, malheureusement.
Regardez l'ordre des ensembles de la théorie des ensembles.




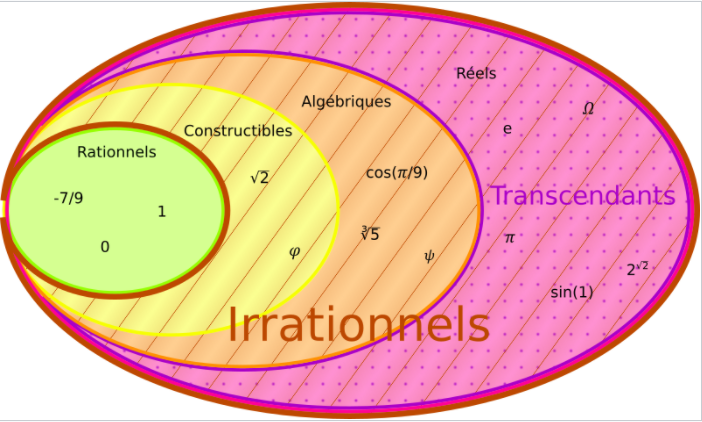
Tout ce qui est dans l'ensemble des "constructibles" (c'est à dire géométriquement constructible) est également dans l'ensemble des "algébriques".
En fait la géométrie c'est beau, mais on peut faire tout ce qui est accessible à la géométrie sans la géométrie, en utilisant seulement l'algèbre.

Par contre, Pi n'est pas constructible et il n'est pas non plus algébrique, donc non seulement on ne peut pas le représenter graphiquement, mais on ne peut pas non plus le remplacer par un polynôme à coefficient rationnel.

Au final, que cela soit sous forme d'une représentation par le segment de droite de la diagonale d'un carré, d'une représentation en trois segments égaux, ou par celle d'une représentation par un cercle pour Pi, on obtient bien un tracé fini qui dans chacun des cas n'est pas numérique.

A partir d'une construction géométrique ou d'un calcul algébrique, on peut obtenir 4 à partir de racine de 2, et même sans savoir écrire racine de 2 on aura la valeur parfaitement exacte de 4.
2 x (2^0.5)^2 = 4

Une opération entre des nombres algébriques qu'on ne peut pas numériser peut parfois donner des résultats entiers.

Une opération entre des nombres algébriques et un nombre transcendant ne donnera jamais un résultat accessible.
Le transcendant est un point de non retour dans l'inconnaissable.

Un nombre, c'est une double abstraction : Puisqu'il s'abstrait à la fois d'une forme numérique, et d'une dimension géométrique pratique (qui est donc de l'ordre de l'idéal)

Une partie des rationnels est au delà des entiers.
Une partie des constructible est au delà des rationnels.
Une partie des algébriques est au delà des constructibles.
Une partie des transcendants est au delà des algébriques.

Les entiers, les rationnels, les constructibles et les algébriques sont dénombrables, avec le bon coefficient, on peut revenir vers les entiers à partir des algébriques car on ne perd pas d'information même si on ne peut pas toujours les écrire numériquement. La quantité d'informations contenue dans un algébrique est finie, même si la notation numérique est infini, toute l'information sur ces nombres est connaissable, parce que tous ces nombres algébriques sont dénombrables entre eux.


Les transcendants sont non dénombrables, ils ont entre eux la puissance du continu, ils ne sont pas dénombrables mais ils sont différenciés, ils ont chacun une valeur propre et ils sont ordonnés les uns après les autres, mais comme ils ne sont pas dénombrables, pour les différencier il faut avoir une précision infinie, dès lors, et c'est là qu'est le problème, la quantité d'information pour définir entièrement un transcendant est infinie, et on n'a pas la possibilité de connaître autant d'informations, si bien, les transcendants sont in fine inconnaissables.

Un nombre n'est pas quelque chose qui doit obligatoirement être numérisable ou bien dénombrable ou même connaissable, c'est seulement une quantité déterminée non variable et finie.

Pi est une quantité déterminée et finie, cela suffit pour en faire un nombre, même si on ne peut pas exactement connaître ce nombre.


Prenons une droite qu'on nome "l'axe des x" qui est bijective sur l'ensemble des réels tel que la proportion entre les nombres soit la proportion entre les distances sur l'axe.
Pi se trouve sur cet axe, en un seul endroit et toujours au même endroit, on ne sait pas le trouver exactement, mais on sait que Pi est une constante, cela suffit pour en faire un nombre réel.

[neopilina]

Il y a l'espace d'un instant.

L'instant est un miroir aux alouettes, un piège terrible, une vue de l'esprit, c'est de la durée, c'est à dire une mesure. Une mesure encore plus trompeuse que les autres. Je m'explique, une mesure est bornée par deux limites, deux jalons, etc., par exemple sur une règle, je vois, je regarde, un " 6 " et un " 7 ", entre les deux il est convenu de dire qu'il y a un centimètre. Comme pour toute mesure, tu peux potentiellement infiniment penser plus précis, plus petit. La durée, cette mesure, là, celle du temps, comporte une difficulté supplémentaire : les deux jalons, limites, sont plantés sur un " tapis roulant ", le temps, qui ne cesse pas de s'écouler pendant que je mesure (je jette un oeil sur ma règle qui, elle, n'a pas bougée !). Le temps est un infini en acte, oui !, mais il faut préciser : tant qu'il durera !!    

Le problème est qu'on a beaucoup de difficulté à penser un espace vide.

Pas du tout. L'univers, c'est surtout du vide sidéral, avec quelques photons, un tout petit peu de lumière, d'astres lumineux lointains.

[Contenu sponsorisé]