L'infini est-il limité ?
+7
quid
hks
Vanleers
neopilina
Magni
jean tardieu
Leonhard
11 participants
Page 5 sur 9
Page 5 sur 9 •  1, 2, 3, 4, 5, 6, 7, 8, 9
1, 2, 3, 4, 5, 6, 7, 8, 9 
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Certes, placé au milieu d'un échiquier,leonhard a écrit:Mais tu ne saurais rien faire au milieu de nombres rationnels si tu ne connaissais pas leur définition.
je ne sais rien faire si j'ignore les règles du jeu.
Mais placé au milieu de l'infini, je sais très bien vivre sans en avoir de définition.
De plus, je n'en éprouve pas le besoin.
Est- ce qu'un amoureux éprouve le besoin d'une définition de l'amour ?
hks- Digressi(f/ve)

- Nombre de messages : 12518
Date d'inscription : 04/10/2007
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Leonhard a écrit:Tu te trompes.Vanleers a écrit:chaque intervalle tend vers un point dont l’abscisse est rationnelle
Tu supposes à tort qu'une suite de nombres rationnels (les extrémités des intervalles) doit nécessairement tendre vers un nombre rationnel.
Mais c'est faux, et voici un contre-exemple simple. Considère un nombre irrationnel quelconque, disons pi. Prends alors la suite des écritures décimales de pi que tu tronques à la n-ème décimale :
- 3
- 3,1
- 3,14
- 3,141
- 3,1415
- 3,14159
- 3,141592
- etc.
Chacun de ces nombres est rationnel, pourtant cette suite tend par construction vers pi qui est un irrationnel. Il s'agit de la propriété générale de la densité des rationnels dans les réels : elle affirme que tout réel (y compris tout irrationnel) est la limite d'une suite de rationnels.
Autre preuve que tu te trompes :
Dans le processus de subdivision du segment [0,1], tu peux choisir n'importe quel irrationnel de [0,1], disons pi. À chaque étape N, pi se trouve dans l'un des intervalles. Considère alors la suite des intervalles qui contiennent pi.
Ces intervalles sont de plus en plus étroits, leur largeur tend vers zéro, et ils contiennent tous pi. Cela signifie précisément que ces intervalles finissent par se refermer sur pi, ils "deviennent" le singleton {pi} lorsqu'on pousse le processus à l'infini. Ce qui prouve que pi n'a pas été "mis de côté" dans le processus. Et comme ce raisonnement vaut pour n'importe quel nombre de [0,1] (irrationnel ou pas), cela prouve que tous les nombres de [0,1] sont capturés. CQFD.
Vous faites une erreur de raisonnement.
Soit E l’ensemble des nombres rationnels (quotients de deux entiers) compris entre 0 et 1.
Soit x un nombre irrationnel compris entre 0 et 1.
x n’appartient pas à E et pourtant on démontre que :
Quel que soit ε aussi petit que l’on veut, on peut trouver des nombres rationnels p et q tels que :
q - p < ε
p < x < q
Autrement dit, on peut approcher x d’aussi près que l’on veut par des nombres rationnels, bien que x ne soit pas rationnel.
Le procédé consistant à faire une partition du segment 0 1 en N intervalles de longueur 1/N et à faire tendre N vers l’infini consiste, comme je l’ai montré, à construire l’ensemble des points de 0 1 ayant une abscisse rationnelle.
Cette construction laisse échapper les nombres irrationnels bien que, comme rappelé ci-dessus, chacun de ces nombres puisse être approché d’aussi près que l’on veut par un nombre rationnel.
Une construction qui laisse échapper la « quasi totalité » des points du segment ne peut être dite une construction du segment.
Vanleers- Digressi(f/ve)

- Nombre de messages : 4217
Date d'inscription : 15/01/2017
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Je l'ai déjà dit dans mon message, c'est la propriété de densité des rationnels dans les réels.Vanleers a écrit:Vous faites une erreur de raisonnement.
Soit E l’ensemble des nombres rationnels (quotients de deux entiers) compris entre 0 et 1.
Soit x un nombre irrationnel compris entre 0 et 1.
x n’appartient pas à E et pourtant on démontre que :
Quel que soit ε aussi petit que l’on veut, on peut trouver des nombres rationnels p et q tels que :
q - p < ε
p < x < q
Autrement dit, on peut approcher x d’aussi près que l’on veut par des nombres rationnels, bien que x ne soit pas rationnel.
Ton raisonnement est erroné et je l'ai démontré en donnant un contre-exemple, ainsi qu'une preuve directe. Je vois que tu ne les as pas compris.Vanleers a écrit:Le procédé consistant à faire une partition du segment 0 1 en N intervalles de longueur 1/N et à faire tendre N vers l’infini consiste, comme je l’ai montré, à construire l’ensemble des points de 0 1 ayant une abscisse rationnelle.
Je crois que tu as oublié de considérer que si on a un intervalle [a, b], il contient tous les nombres (même irrationnels) compris entre a et b, et cela même si a et b sont rationnels.
Dans les deux derniers paragraphes de mon message, j'explique comment on peut exhiber une suite d'intervalles qui se referment sur n'importe quel irrationnel au choix de [0,1], ce qui montre que tout irrationnel fait bien partie des "intervalles infiniment étroits" que l'on obtient prenant la limite pour N tendant vers l'infini.
Leonhard- Digressi(f/ve)

- Nombre de messages : 194
Date d'inscription : 03/09/2007
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Les rationnels sont dénombrables, les réels sont indénombrables.
Quel que soit le rationnel considéré, aussi proche soit il d'un nombre x transcendant, il y aura toujours une infinité de nombres transcendants plus grands que ce rationnel et plus petit que x.
On ne peut pas approcher un transcendant avec un rationnel de sorte qu'on puisse trouver un rationnel qui touche le transcendant de la façon dont les transcendants se touchent entre eux de façon continue.
La succession des rationnels n'est pas une succession continue.
Entre 3 et Pi il y a une infinité de réels.
Entre 3,14 et Pi il y a une infinité de réels.
Entre 3,1415926526 et Pi il y a une infinité de réels.
Et ainsi de suite jusqu'à 31 trillion des décimales de Pi déjà calculées, et on peut calculer autant de décimales qu'on veut, cela n'y changera rien, il y aura toujours une infinité de réels plus grands que la valeur approchée calculée de Pi et la valeur exacte de Pi.
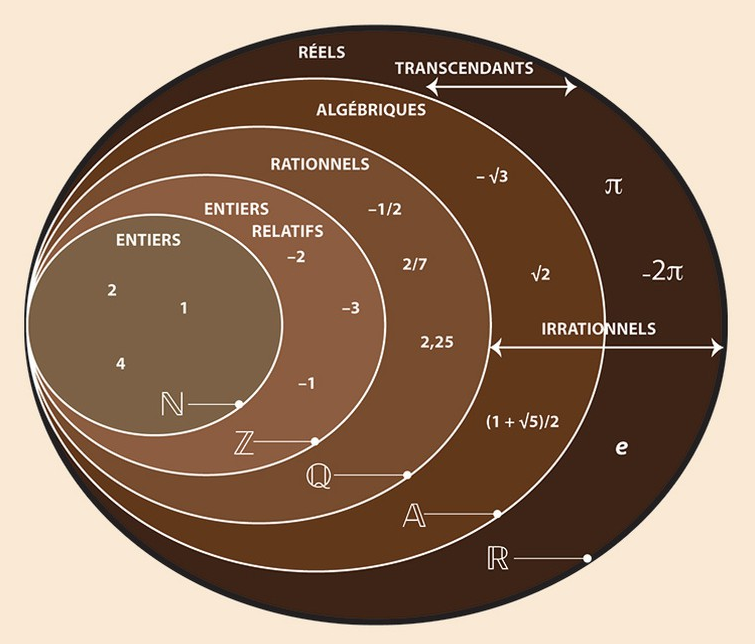
Quel que soit le rationnel considéré, aussi proche soit il d'un nombre x transcendant, il y aura toujours une infinité de nombres transcendants plus grands que ce rationnel et plus petit que x.
On ne peut pas approcher un transcendant avec un rationnel de sorte qu'on puisse trouver un rationnel qui touche le transcendant de la façon dont les transcendants se touchent entre eux de façon continue.
La succession des rationnels n'est pas une succession continue.
Entre 3 et Pi il y a une infinité de réels.
Entre 3,14 et Pi il y a une infinité de réels.
Entre 3,1415926526 et Pi il y a une infinité de réels.
Et ainsi de suite jusqu'à 31 trillion des décimales de Pi déjà calculées, et on peut calculer autant de décimales qu'on veut, cela n'y changera rien, il y aura toujours une infinité de réels plus grands que la valeur approchée calculée de Pi et la valeur exacte de Pi.

_________________
Ce que je dis n'engage que moi.

Magni- Digressi(f/ve)

- Nombre de messages : 1065
Localisation : 62100
Date d'inscription : 03/05/2016
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Leonhard a écrit:ce qui montre que tout irrationnel fait bien partie des "intervalles infiniment étroits" que l'on obtient prenant la limite pour N tendant vers l'infini.
Je ne sais pas ce que tu entends par "intervalle infiniment étroit", mais si un intervalle entre deux réels est non nul, il contient une infinité de réels.
D'autre part, si on pouvait obtenir qu'un rationnel soit contigu (touche) un réel, alors cela démontrerait que ce réel n'est PAS un transcendant mais un rationnel.
Les transcendants ne font PAS partie de l'ensemble des rationnels.
Toute démonstration qui montrerait autre chose serait absurde du point de vue des axiomes de la théorie des ensembles.
_________________
Ce que je dis n'engage que moi.

Magni- Digressi(f/ve)

- Nombre de messages : 1065
Localisation : 62100
Date d'inscription : 03/05/2016
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Ça reste vrai si tu remplaces "transcendant" (en rouge) par "rationnel". Ce n'est pas cette propriété qui distingue les rationnels (dénombrables) des irrationnels (indénombrables).Magni a écrit:Quel que soit le rationnel considéré, aussi proche soit il d'un nombre x transcendant, il y aura toujours une infinité de nombres transcendants plus grands que ce rationnel et plus petit que x.
Ce langage n'a aucun sens, car aucun nombre ne touche aucun autre nombre (rationnels ou pas). Quels que soient deux nombres a et b, il existe toujours une infinité de nombres (rationnels et irrationnels) entre eux. Il n'y a pas deux nombres qui soient des "voisins directs".Magni a écrit:On ne peut pas approcher un transcendant avec un rationnel de sorte qu'on puisse trouver un rationnel qui touche le transcendant de la façon dont les transcendants se touchent entre eux de façon continue.
La continuité, ce n'est pas que "les nombres se touchent", c'est que "il n'y a pas de trou". Mais je vois que ce point pose problème chez plusieurs membres, donc on va l'éclaircir dans un autre sujet.
Cela ne se produirait jamais puisqu'aucun nombre ne touche/n'est contigu à aucun autre nombre.Magni a écrit:D'autre part, si on pouvait obtenir qu'un rationnel soit contigu (touche) un réel, alors cela démontrerait que ce réel n'est PAS un transcendant mais un rationnel.
C'est la limite d'une suite d'intervalles dont la largeur tend vers zéro. Une telle limite est, en fait, un singleton, c'est-à-dire un intervalle dont les deux extrémités sont égales. Un tel intervalle contient un unique nombre. Exemple : [3, 3] = {3}.Magni a écrit:Je ne sais pas ce que tu entends par "intervalle infiniment étroit", mais si un intervalle entre deux réels est non nul, il contient une infinité de réels.
Leonhard- Digressi(f/ve)

- Nombre de messages : 194
Date d'inscription : 03/09/2007
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Leonhard a écrit:Ce langage n'a aucun sens, car aucun nombre ne touche aucun autre nombre (rationnels ou pas). Quels que soient deux nombres a et b, il existe toujours une infinité de nombres (rationnels et irrationnels) entre eux. Il n'y a pas deux nombres qui soient des "voisins directs".Magni a écrit:On ne peut pas approcher un transcendant avec un rationnel de sorte qu'on puisse trouver un rationnel qui touche le transcendant de la façon dont les transcendants se touchent entre eux de façon continue.
Est ce que tu veux dire que tu es d'accord sur le fait qu'un rationnel ne peut pas approcher un réel transcendant ?
Est ce que tu veux dire que tu pratiques une sorte de math dans laquelle les rationnels sont indénombrables ?
_________________
Ce que je dis n'engage que moi.

Magni- Digressi(f/ve)

- Nombre de messages : 1065
Localisation : 62100
Date d'inscription : 03/05/2016
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Pas du tout. On peut approcher un transcendant d'aussi près que l'on veut par un rationnel.Magni a écrit:Est ce que tu veux dire que tu es d'accord sur le fait qu'un rationnel ne peut pas approcher un réel transcendant ?
Évidemment que non. Les rationnels sont dénombrables. Et, en même temps, on peut approcher n'importe quel nombre réel d'aussi près que l'on veut avec des rationnels. Autrement dit, les rationnels sont à la fois dénombrables et denses dans les réels.Magni a écrit:Est ce que tu veux dire que tu pratiques une sorte de math dans laquelle les rationnels sont indénombrables ?
Leonhard- Digressi(f/ve)

- Nombre de messages : 194
Date d'inscription : 03/09/2007
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
hks a écrit:
Je comprends bien ce que le discours philosophique puisse sembler parfois nébuleux à un esprit de géométrie. A l'inverse les mathématiques peuvent sembler parfois un peu hors sujet ou à côté des interrogations philosophiques.
Mathématiques signifiantes en leur monde et en les mondes qu'elles innervent, mais pas en dehors.
La physique (comme science dure) est incluse dans ce monde mathématique quand elle dépend des équations. La physique est totalement colonisée par /inféodée aux /gouvernée par les mathématiques.
La physique est signifiante, certes elle apporte du sens ...mais pas tout ce qu'il est possible à un esprit humain de créer comme sens (signification).
Hélas la physique produit aussi souvent comme un effet d'assèchement.
Je suis assez d’accord avec ce que vous écrivez.
Le monde est plus riche que ce peuvent en dire les mathématiques et la physique.
Une approche holistique prendra en considération non seulement la dimension intellectuelle mais aussi les dimensions affective et corporelle du monde.
C’est cette approche globale qui nourrit son homme (et le rafraîchit).
Vanleers- Digressi(f/ve)

- Nombre de messages : 4217
Date d'inscription : 15/01/2017
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
(
Bon éléate, en tous cas on assez vu que je m'y efforce (il y a une trentaine d'années quand " ça " m'a pris, j'ai passé un " certain temps " a rassemblé à peu près tout ce qui existait en français pour cette littérature spécialisée), mon postulat, ontologique et donc dialectique, est celui-ci : l'infini est absolument partout, potentiellement, dans les formalisations, les verbalisations, les " discours ", en commençant par les plus basiques : mes sensations, mes perceptions, etc. Là, tout de suite, si je m'en donne la peine, je pourrais en faire l'expérience en examinant par exemple mon champ de vision, etc. L'infini circule. Ontologiquement et donc dialectiquement, un Etant est un numériquement et Un en terme de cohérence dialectique pour pouvoir être, faire sens et/ou Sens. Et donc je m'intéresse à l'infini, à cette circulation, etc. Et j'ai bien constaté que le formalisme qui s'est le mieux et le plus coltiné l'infini, c'est les mathématiques. Alors, les mathématiques s'aperçoivent qu'elles rencontrent des difficultés (1) avec l'infini, " l'animal est rétif ", mais cela même est édifiant, intéressant.
Alors je continue à remercier nos trois matheux et à les lire avec la plus grande attention. Je vais faire scanner mon petit " dossier " à ce sujet, et chacun, comme il se doit, en fera ce qu'il lui plaira.
(1)
)
Bon éléate, en tous cas on assez vu que je m'y efforce (il y a une trentaine d'années quand " ça " m'a pris, j'ai passé un " certain temps " a rassemblé à peu près tout ce qui existait en français pour cette littérature spécialisée), mon postulat, ontologique et donc dialectique, est celui-ci : l'infini est absolument partout, potentiellement, dans les formalisations, les verbalisations, les " discours ", en commençant par les plus basiques : mes sensations, mes perceptions, etc. Là, tout de suite, si je m'en donne la peine, je pourrais en faire l'expérience en examinant par exemple mon champ de vision, etc. L'infini circule. Ontologiquement et donc dialectiquement, un Etant est un numériquement et Un en terme de cohérence dialectique pour pouvoir être, faire sens et/ou Sens. Et donc je m'intéresse à l'infini, à cette circulation, etc. Et j'ai bien constaté que le formalisme qui s'est le mieux et le plus coltiné l'infini, c'est les mathématiques. Alors, les mathématiques s'aperçoivent qu'elles rencontrent des difficultés (1) avec l'infini, " l'animal est rétif ", mais cela même est édifiant, intéressant.
Alors je continue à remercier nos trois matheux et à les lire avec la plus grande attention. Je vais faire scanner mon petit " dossier " à ce sujet, et chacun, comme il se doit, en fera ce qu'il lui plaira.
(1)
Leonhard a écrit:Vous êtes nombreux à avoir fait des calculs avec l'infini. Mais il faut savoir que d'un point de vue algébrique, l'ajout des infinis exige de renoncer à des propriétés algébriques classiques, avec pour conséquence que l'on ne peut pas vraiment calculer avec les infinis.
Dans ton exemple [Vanleers"], considérons l'équation NQ=Q (où on suppose que N>1). Elle est équivalente à (N-1)Q=0, et la seule solution algébrique est Q=0. Si ∞ était aussi une solution, on aurait une contradiction car, d'une part, on aurait que (N-1)∞=0 mais, d'autre part, l'infini multiplié par un nombre non nul reste l'infini, c.-à-d. que (N-1)∞=∞. Il en découlerait que 0=∞ ce qui est contradictoire.
De façon générale, on ne peut même pas vraiment dire que ∞=∞ puisque ∞-∞ n'est pas égal à zéro, c'est ce qu'on appelle une forme indéterminée. Ceci indique que non seulement l'infini n'est pas un nombre, mais qu'en plus il n'a même pas d'identité fixe.
Pour ce genre de raisons, réfléchir sur base de calculs approximatifs avec des infinis, c'est tomber rapidement dans des élucubrations insensées.
)
_________________
" Tout Étant produit par moi m'est donné (c'est son statut philosophique), a priori, et il est Mien (cogito, conscience de Soi, libéré du Poêle) ". " Savoir guérit, forge. Et détruit tout ce qui doit l'être ", ou, équivalents, " Tout l'Inadvertancier constitutif doit disparaître ", " Le progrès, c'est la liquidation du Sujet empirique, notoirement névrotique, par la connaissance ". " Il faut régresser et recommencer, en conscience ". Moi.
C'est à pas de colombes que les Déesses s'avancent.

neopilina- Digressi(f/ve)

- Nombre de messages : 8364
Date d'inscription : 31/10/2009
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Ma capacité à réfléchir sur l'infini est très limitée ! Merci pour vos apports.
_________________
‚καλούμενός τε κἄκλητος θεὸς παρέσται'
Vocatus atque non vocatus deus aderit
Invoqué ou non, Dieu sera là.

Jans- Digressi(f/ve)

- Nombre de messages : 558
Localisation : IdF
Date d'inscription : 27/09/2017
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Je crois que nous sommes tous d'accord,il faut dire merci.
Cependant tout ça reste très nébuleux.
L'infini , à 11/12 ans c'était allongé au sol, à regarder le ciel, la nuit et le jour, ça change rien à la question.
Tout ça reste très vertigineux, quelque soit les tentatives d'explication.
Les maths comme une possibilité de résolution ?
Je ne suis pas sur du tout.
Je crois savoir qu'il y a des anges, des angles morts.
Je pense au film Interstellar.
Où Solaris dans sa première version.
J'apprécie les contribuables des matheux.
Merci.
Sans vouloir polluer.
Cependant tout ça reste très nébuleux.
L'infini , à 11/12 ans c'était allongé au sol, à regarder le ciel, la nuit et le jour, ça change rien à la question.
Tout ça reste très vertigineux, quelque soit les tentatives d'explication.
Les maths comme une possibilité de résolution ?
Je ne suis pas sur du tout.
Je crois savoir qu'il y a des anges, des angles morts.
Je pense au film Interstellar.
Où Solaris dans sa première version.
J'apprécie les contribuables des matheux.
Merci.
Sans vouloir polluer.
_________________
Soyez patient envers tout ce qui n'est pas résolu dans votre cœur et essayez d'aimer les questions elles-mêmes

lanK- Digressi(f/ve)

- Nombre de messages : 458
Date d'inscription : 12/09/2007
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Je reviens à l'exemple de la partition d’un segment de droite [0 1] de longueur 1 en N intervalles de longueur 1/N quand N tend vers l’infini.
Ce segment est un ensemble infini de points, chaque point étant repéré par son abscisse : un nombre compris entre 0 et 1.
On est donc en présence d’ un ensemble infini de nombres compris entre 0 et 1.
Cantor a montré qu’un tel ensemble est indénombrable (argument dit de la diagonale) et a appelé c sa puissance : puissance (ou cardinal) du continu.
Quel que soit N, dans chaque intervalle, on est en présence d’un ensemble infini de nombres, ensemble dont la puissance est égale à c car on peut toujours construire une bijection entre cet ensemble et l’ensemble des nombres compris entre 0 et 1.
De façon imagée (mais, en toute rigueur, impropre), dans tout intervalle, aussi infime soit-il, on est toujours en présence du même nombre infini de nombres.
On voit, sur cet exemple, la différence entre un infini en acte : l’infini d’un ensemble de nombres considérés simultanément et l’infini en puissance : le nombre N qui peut être aussi grand que l’on veut.
Ce segment est un ensemble infini de points, chaque point étant repéré par son abscisse : un nombre compris entre 0 et 1.
On est donc en présence d’ un ensemble infini de nombres compris entre 0 et 1.
Cantor a montré qu’un tel ensemble est indénombrable (argument dit de la diagonale) et a appelé c sa puissance : puissance (ou cardinal) du continu.
Quel que soit N, dans chaque intervalle, on est en présence d’un ensemble infini de nombres, ensemble dont la puissance est égale à c car on peut toujours construire une bijection entre cet ensemble et l’ensemble des nombres compris entre 0 et 1.
De façon imagée (mais, en toute rigueur, impropre), dans tout intervalle, aussi infime soit-il, on est toujours en présence du même nombre infini de nombres.
On voit, sur cet exemple, la différence entre un infini en acte : l’infini d’un ensemble de nombres considérés simultanément et l’infini en puissance : le nombre N qui peut être aussi grand que l’on veut.
Vanleers- Digressi(f/ve)

- Nombre de messages : 4217
Date d'inscription : 15/01/2017
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Exact. Mais passer à la limite pour N tendant vers l'infini, c'est précisément faire un saut par-dessus l'infinité d'étapes pour atteindre leur horizon.Vanleers a écrit:De façon imagée (mais, en toute rigueur, impropre), dans tout intervalle, aussi infime soit-il, on est toujours en présence du même nombre infini de nombres.
Par exemple, on sait que la limite de 1/M vaut zéro quand M tend vers l'infini. Aucun des 1/M ne vaut zéro. Et pourtant, cette limite, elle, est strictement égale à zéro. La limite d'une suite n'est pas un terme de cette suite, aussi loin soit-il dans la suite; la limite est ce qui est au-delà de tous les termes, un nombre dont se rapproche indéfiniment, d'aussi près que l'on veut à condition d'aller loin dans la suite.
De même, dans les subdivisions successives de [0,1], aucun des intervalles à une étape N donnée n'est réduit à un seul nombre. Mais la limite de ces intervalles n'est pas l'un de ceux-ci, elle est ce vers quoi ceux-ci tendent, et est exactement un singleton, c.-à-d. un intervalle d'un seul nombre.
Le calcul des limites a déjà des relents d'infini actuel.
Leonhard- Digressi(f/ve)

- Nombre de messages : 194
Date d'inscription : 03/09/2007
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Non, aussi petit soit-il, chaque intervalle est un ensemble infini de nombres et ne se referme jamais sur un seul nombre.
Ce n’est pas en faisant une partition du segment [0 1] en N intervalles et en faisant tendre N à l’infini que l’on construit les nombres réels.
Car les nombres réels doivent être construits et plusieurs mathématiciens s’y sont employés.
Citons les suites de Cauchy et les coupures de Dedekind.
Mais ce forum n’est pas un forum de mathématiques et je doute que ces questions techniques intéressent les « honnêtes hommes » qui le fréquentent.
Ce n’est pas en faisant une partition du segment [0 1] en N intervalles et en faisant tendre N à l’infini que l’on construit les nombres réels.
Car les nombres réels doivent être construits et plusieurs mathématiciens s’y sont employés.
Citons les suites de Cauchy et les coupures de Dedekind.
Mais ce forum n’est pas un forum de mathématiques et je doute que ces questions techniques intéressent les « honnêtes hommes » qui le fréquentent.
Vanleers- Digressi(f/ve)

- Nombre de messages : 4217
Date d'inscription : 15/01/2017
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Si on prend la limite de la suite des intervalles, cette limite est bien un singleton ne contenant qu'un seul nombre.Vanleers a écrit:Non, aussi petit soit-il, chaque intervalle est un ensemble infini de nombres et ne se referme jamais sur un seul nombre.
Il y a plusieurs méthodes équivalentes pour construire les nombres réels : par les suites de Cauchy, les coupures de Dedekind, mais aussi les limites de suites d'intervalles dont la largeur tend vers zéro.Vanleers a écrit:Ce n’est pas en faisant une partition du segment [0 1] en N intervalles et en faisant tendre N à l’infini que l’on construit les nombres réels.
Car les nombres réels doivent être construits et plusieurs mathématiciens s’y sont employés.
Citons les suites de Cauchy et les coupures de Dedekind.
Ma parole ne vaut rien puisque je ne suis qu'un inconnu sur un forum, donc voici quelques sources extérieures :
- (En anglais) Les différentes propriétés équivalentes à la "continuité" (en fait, la complétude) des nombres réels :
https://en.wikipedia.org/wiki/Completeness_of_the_real_numbers
La 4e propriété de la liste est la propriété des intervalles emboîtés, disant qu'une suite d'intervalles emboîtés dont la largeur tend vers zéro possède une intersection (qui est la limite de la suite) qui se réduit à un seul élément. Dans un message précédent, je t'ai exhibé une suite d'intervalles contenant tous un nombre irrationnel, et cette suite tend vers le singleton réduit à cet irrationnel seul, prouvant par là que cet irrationnel est bien l'un des nombres obtenus par ce processus. (Et c'est vrai pour tout autre nombre, irrationnel ou pas.) - Théorème des intervalles emboîtés :
http://www.bibmath.net/dico/index.php?action=affiche&quoi=./s/segemboites.html
Une page en français, qui dit la même chose que ci-dessus.
Ce n'est pas une raison pour ne pas rectifier des affirmations fausses :) L'"honnête homme" valorise la pensée rigoureuse, qu'il soit compétent ou pas sur une question.Vanleers a écrit:Mais ce forum n’est pas un forum de mathématiques et je doute que ces questions techniques intéressent les « honnêtes hommes » qui le fréquentent.
Leonhard- Digressi(f/ve)

- Nombre de messages : 194
Date d'inscription : 03/09/2007
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Leonhard a écrit:Si on prend la limite de la suite des intervalles, cette limite est bien un singleton ne contenant qu'un seul nombre.Vanleers a écrit:Non, aussi petit soit-il, chaque intervalle est un ensemble infini de nombres et ne se referme jamais sur un seul nombre.
Vous n’avez rien démontré du tout. Je vous cite :Leonhard a écrit:Dans le processus de subdivision du segment [0,1], tu peux choisir n'importe quel irrationnel de [0,1], disons pi. À chaque étape N, pi se trouve dans l'un des intervalles. Considère alors la suite des intervalles qui contiennent pi.
Ces intervalles sont de plus en plus étroits, leur largeur tend vers zéro, et ils contiennent tous pi. Cela signifie précisément que ces intervalles finissent par se refermer sur pi, ils "deviennent" le singleton {pi} lorsqu'on pousse le processus à l'infini. Ce qui prouve que pi n'a pas été "mis de côté" dans le processus. Et comme ce raisonnement vaut pour n'importe quel nombre de [0,1] (irrationnel ou pas), cela prouve que tous les nombres de [0,1] sont capturés. CQFD.
Vous vous contentez d’affirmer, sans aucun argument, que le nombre Pi, disons Pi – 3 pour rester dans le segment [0 1], parce qu’il est un élément de tous les ensembles infinis correspondant à des intervalles de plus en plus petits est le seul nombre ayant cette propriété.
Il faudrait le montrer car comment est-il possible que les intervalles qui, quelle que soit leur largeur, sont toujours des ensembles infinis de nombres, « finissent » par se refermer sur un nombre unique, alors que ça ne finit jamais (N est toujours aussi grand que l'on veut).
Je ne doute pas pas que les mathématiciens ont construit ce nombre mais ce que vous en avez dit est sans rigueur et trop sommaire pour qu’on puisse le comprendre.
Vanleers- Digressi(f/ve)

- Nombre de messages : 4217
Date d'inscription : 15/01/2017
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Leonhard a écrit:Si on prend la limite de la suite des intervalles, cette limite est bien un singleton ne contenant qu'un seul nombre.Vanleers a écrit:Non, aussi petit soit-il, chaque intervalle est un ensemble infini de nombres et ne se referme jamais sur un seul nombre.
On ne peut pas obtenir un nombre transcendant avec une suite qui converge vers un nombre rationnel.
Dés lors, le nombre transcendant qui est visé et le nombre rationnel obtenu sont deux nombres différents.
Leonhard a écrit:aucun nombre ne touche aucun autre nombre (rationnels ou pas). Quels que soient deux nombres a et b, il existe toujours une infinité de nombres (rationnels et irrationnels) entre eux. Il n'y a pas deux nombres qui soient des "voisins directs".
D'autre part, les nombres transcendants sont "non constructibles et non algébriques", l'infini n'a toujours pas été "achevé", personne n'a fait ni ne fera avant un temps infini un calcul avec une infinité d'itérations.
Une suite qui converge vers un nombre transcendant après une infinité d'itérations n'abouti pas.
Nous avons cette suite pour calculer des décimales de Pi, c'est la "formule de Leibniz-Grégory".
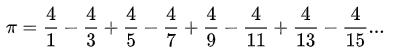
Voila, cette suite se "referme" sur Pi, quand ? Après une infinité d'itérations, c'est à dit : jamais !
Si une suite converge vers un nombre transcendant, cette suite permet de calculer autant de décimales du nombre transcendant que l'on veut aussi longtemps que ce nombre de décimales est un nombre réel et non pas une quantité infinie.
Avec une suite, on ne peut qu'obtenir un nombre algébrique, on n'obtiendra pas un nombre transcendant qui est non algébrique !
La limite de la formule de Leibniz-Grégory est bien un singleton et c'est Pi, mais jamais vous ne pourrez calculer ce nombre qui est non algébrique.
Dire qu'il "suffit" de prendre ce nombre pour obtenir Pi c'est c'est inconsistant, car ce n'est pas possible.
Il faut revenir aux bases que sont les notions de physique et métaphysique et faire la différence entre potentiel et actuel.
Personne n'a réalisé l'infini en acte et personne n'a encore trouvé le moyen de faire une itération à l'infini "en acte".
Dernière édition par Magni le Mar 20 Avr 2021 - 17:34, édité 2 fois
_________________
Ce que je dis n'engage que moi.

Magni- Digressi(f/ve)

- Nombre de messages : 1065
Localisation : 62100
Date d'inscription : 03/05/2016
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Il suffit d'appliquer le théorème des segments emboîtés et d'arranger un peu la subdivision, et c'est fait. Mais c'est vrai que le niveau de détail suffisant dépend des acquis du lecteur.Vanleers a écrit:Il faudrait le montrer car comment est-il possible que les intervalles qui, quelle que soit leur largeur, sont toujours des ensembles infinis de nombres, « finissent » par se refermer sur un nombre unique, alors que ça ne finit jamais (N est toujours aussi grand que l'on veut).
Si tu veux, voici une démonstration académique :
Considérons le processus de subdivision suivant :
- On commence à l'étape 1 avec l'intervalle [0,1].
- À chaque étape N, on divise chaque intervalle obtenu à l'étape précédente en deux sous intervalles de même largeur.
Par exemple, à l'étape 3, on a les points de subdivision 0, 1/4, 2/4, 3/4, 1. À l'étape 4, on a les points de subdivision 0, 1/8, 2/8, ..., 7/8, 1.
Ce processus de subdivision a l'avantage que chaque intervalle à une étape donnée est d'emblée inclus dans un intervalle à l'étape précédente, ce qui facilitera l'usage du théorème des segments emboîtés. Mais il est essentiellement analogue à celui qu'on a discuté : toutes les extrémités des intervalles sont des nombres rationnels, les intervalles se resserrent, mais à chaque étape N, tout intervalle contient toujours une infinité d'éléments.
Choisissons maintenant un nombre irrationnel arbitraire, par exemple pi-3 comme tu as proposé.
À chaque étape N, pi-3 fait partie d'un des intervalles de la subdivision. Notons cet intervalle IN. Considérons alors la suite de tous les intervalles IN quand N augmente.
Par construction, chaque IN est contenu dans IN-1, donc on a bien une suite d'intervalles emboîtés. De plus, la largeur de ces intervalles tend vers 0 (puisqu'elle est divisée par deux à chaque étape). Par le théorème des segments emboîtés, l'intersection infinie de tous ces intervalles est un singleton ne contenant qu'un seul nombre. Or, par construction, pi-3 fait partie de tous ces intervalles. Donc l'intersection de tous ces intervalles contient comme unique élément le nombre pi-3.
Cette intersection est, intuitivement, l'intervalle vers lequel les intervalles IN tendent, bien qu'elle ne soit pas elle-même l'un de ces IN. Et on vient de démontrer qu'il s'agit précisément d'un singleton contenant l'irrationnel pi-3. Comme pi-3 était arbitrairement choisi, ceci montre que tout irrationnel (en fait, tout réel) est bel et bien la limite d'une suite d'intervalles qui se resserrent.
CQFD.
Leonhard- Digressi(f/ve)

- Nombre de messages : 194
Date d'inscription : 03/09/2007
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Évidemment. Mais on peut obtenir un nombre transcendant avec une suite qui converge vers un nombre transcendant.Magni a écrit:On ne peut pas obtenir un nombre transcendant avec une suite qui converge vers un nombre rationnel.
Tu ne comprends tout simplement pas le concept même de limite d'une suite, c'est pour ça que tu es bloqué. La limite d'une suite n'est pas le dernier élément de la suite (qui n'existe pas). La limite d'une suite de nombres est le nombre vers lequel les éléments de la suite tendent continuellement. La limite d'une suite d'intervalles est l'intervalle vers lequel ceux de la suite tendent continuellement.Magni a écrit:Voila, cette suite se "referme" sur Pi, quand ? Après une infinité d'itération, c'est à dit : jamais !
Pourtant, la suite des écritures tronquées de pi :Magni a écrit:Avec une suite, on ne peut qu'obtenir un nombre algébrique, on n'obtiendra pas un nombre transcendant qui est non algébrique !
- 3
- 3,1
- 3,14
- 3,141
- 3,1415
- 3,14159
- ...
converge vers pi, qui est transcendant. Par ailleurs, la propriété de densité des rationnels dans les réels dit au contraire que tout réel (y compris transcendant) est la limite d'une suite de rationnels.
Tu confonds tout. D'une part, affirmer qu'une suite possède une limite n'implique pas que l'on affirme que la limite soit calculable en pratique avec une précision totale. D'autre part, pas besoin d'aller chercher les transcendants, le bête nombre 1/3 est déjà impossible à écrire sous forme décimale puisqu'il contient une infinité de décimales. Tu confonds donc tout : limite de suite, nombre décimal ou non décimal, transcendance, ...Magni a écrit:La limite de la formule de Leibniz-Grégory est bien un singleton et c'est Pi, mais jamais vous ne pourrez calculer ce nombre qui est non algébrique.
En terme de calculabilité (c.-à-d. de possibilité d'être écrit avec une précision arbitraire finie), pi est calculable, tout autant que 1/3 :
https://fr.wikipedia.org/wiki/Nombre_r%C3%A9el_calculable
La transcendance de pi dit seulement qu'il n'est pas solution d'une équation polynômiale, mais il est solution d'autres types d'équations, c'est tout.
Dernière édition par Leonhard le Mar 20 Avr 2021 - 17:46, édité 5 fois
Leonhard- Digressi(f/ve)

- Nombre de messages : 194
Date d'inscription : 03/09/2007
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Pi est un très bon exemple, on n'a pas calculé sa valeur exacte.
Dire qu'il suffit de prendre la valeur de la suite qui donne Pi pour avoir Pi est inconsistant.
Qui a trouvé Pi, quand ?
Dire qu'il suffit de prendre la valeur de la suite qui donne Pi pour avoir Pi est inconsistant.
Qui a trouvé Pi, quand ?
_________________
Ce que je dis n'engage que moi.

Magni- Digressi(f/ve)

- Nombre de messages : 1065
Localisation : 62100
Date d'inscription : 03/05/2016
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Leonhard a écrit:Tu [Magni] confonds tout. D'une part, affirmer qu'une suite possède une limite n'implique pas que l'on affirme que la limite soit calculable en pratique avec une précision totale. D'autre part, pas besoin d'aller chercher les transcendants, le bête nombre 1/3 est déjà impossible à écrire sous forme décimale puisqu'il contient une infinité de décimales. Tu confonds donc tout : limite de suite, nombre décimal ou non décimal, transcendance, ...
J'entends, je suis d'accord, c'est ce que j'avais essayé d'expliquer à lank quand il s'étonnait du titre du fil. Le nombre de décimales de Pi est infini, il n'empêche qu'il est ultra-déterminé, borné, défini, circonscrit, etc. On ne connaîtra jamais cette suite de décimales et pourtant elle " existe ", elle ne peut pas être autre.
A la limite, dans le cadre d'une réflexion en général sur l'infini, on peut dire qu'avec des cas pareils, on a les infinis les mieux, les plus finement définis, circonscrits, tout ceci précisé : les plus " limités ".
_________________
" Tout Étant produit par moi m'est donné (c'est son statut philosophique), a priori, et il est Mien (cogito, conscience de Soi, libéré du Poêle) ". " Savoir guérit, forge. Et détruit tout ce qui doit l'être ", ou, équivalents, " Tout l'Inadvertancier constitutif doit disparaître ", " Le progrès, c'est la liquidation du Sujet empirique, notoirement névrotique, par la connaissance ". " Il faut régresser et recommencer, en conscience ". Moi.
C'est à pas de colombes que les Déesses s'avancent.

neopilina- Digressi(f/ve)

- Nombre de messages : 8364
Date d'inscription : 31/10/2009
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
bien sûr ...magni a écrit:Personne n'a réalisé l'infini en acte et personne n'a encore trouvé le moyen de faire une itération à l'infini "en acte".
Pour revenir à Cantor je cite un article sur "Cantor est les infinis" .
Il faut voir ses distinctions
1) entre infini potentiel et infini actuel
2)dans l'infini actuel entre les transfinis et l'absolu.
Tout ci dessous est cité de l'article
L'infini potentiel se rencontre là où existe une quantité indéterminée, variable, .finie qui croît au-delà ou décroît en deça de toute limite finie.
«Plus généralement, dit Cantor, je parle d'infini potentiel chaque fois qu'il est question
d'une quantité indéterminée capable de recevoir un nombre illimité de
déterminations ,,6.
Au contraire, par infini actuel, il entend une quantité qui, d'une
part, n'est pas variable, mais entièrement (<< in allen seinen Teilen fest und
bestimmt ») fixe et déterminée, donc une véritable constante, et qui, d'autre part.
dépasse en grandeur toute quantité finie de même nature. À titre d'exemple,
Cantor propose, entre autres, l'ensemble de tous les nombres entiers finis. Cet
ensemble, précise-t-il, est une chose en soi et, abstraction faite de la suite
naturelle des nombres qui lui appartiennent, constitue une quantité entièrement
fixe et déterminée, manifestement plus grand que tout nombre
fini 7 •
...........................................................
Cantor considère l'infini potentiel comme un infini impropre, et l'infini actuel comme un infini propre.
.........................
.Partout où Cantor compare les deux types d'infini, il les distingue et
caractérise en assimilant l'infini potentiel à une variable,
et l'infini actuel à une constante. Cette assimilation reflète bien la conception de Cantor9 . Et. en particulier, l'infini actuel apparaît par là comme quelque chose d'essentiellement
achevé, parfait, complet, quelque chose dont toutes les parties sont
simultanément données. Du fait que l'infini actuel est assimilé à une constante, on
est porté à croire qu'il est incapable d'augmentation ou de croissance. Or, selon
Cantor, c'est là une erreur généralement répandue aussi bien dans la philosophie
ancienne et dans la philosophie scolastique qui s'y rattache que dans la
philosophie moderne et contemporaine. En vérité, de préciser Cantor, l'infini
actuel demeure capable de croissance nonobstant sa constance.

Ce point amène toutefois Cantor à reconnaître un double infini actuel: un, capable de croître,
l'autre, incapable de croître. Il appelle le premier transfïnÎ, le second absolu.
Répétons-le, le transfini est un infini actuel qui peut croître et augmenter
«< vermehrbares A.-U. »)
tandis que l'absolu est incapable de la moindre croissance «< unvermehrbares A.-U. »).
Le couple transfini-absolu offre un trait de
ressemblance étroite avec le couple antérieur: infini potentiel et infini actuel. En
effet, de même que l'infini potentiel doit se rattacher à un infini actuel qui lui sert
de fondement, ainsi le transfini, par sa richesse de formes et de structures, tend
avec nécessité vers un absolu qui en est la source.
À la quantité de cet absolu, rien ne saurait être retranché ni ajouté, de sorte
que, quantitativement, c'est un maximum absolu. L'intelligence humaine est trop
faible pour le saisir parfaitement. Il échappe à toute analyse mathématique 12. Cet
absolu est acte pur, l'être absolument simple, souverainement parfait, jouissant
d'une indépendance totale, extérieur à l'univers. Incapable du moindre changement, c'est lui qui réalise de façon parfaite l'infini actuel. En fait, il ne se trouve
qu'en Dieu ou, pour mieux dire, précise Cantor, il est Dieu lui-même dans sa
souveraine perfection l3 • C'est, il va sans dire, un infini incréé.
https://www.erudit.org/fr/revues/ltp/1977-v33-n1-ltp3381/705591ar.pdf
hks- Digressi(f/ve)

- Nombre de messages : 12518
Localisation : Hauts de Seine
Date d'inscription : 04/10/2007
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
Leonhard a écrit:
Par construction, chaque IN est contenu dans IN-1, donc on a bien une suite d'intervalles emboîtés. De plus, la largeur de ces intervalles tend vers 0 (puisqu'elle est divisée par deux à chaque étape). Par le théorème des segments emboîtés, l'intersection infinie de tous ces intervalles est un singleton ne contenant qu'un seul nombre. Or, par construction, pi-3 fait partie de tous ces intervalles. Donc l'intersection de tous ces intervalles contient comme unique élément le nombre pi-3.
Cette intersection est, intuitivement, l'intervalle vers lequel les intervalles IN tendent, bien qu'elle ne soit pas elle-même l'un de ces IN. Et on vient de démontrer qu'il s'agit précisément d'un singleton contenant l'irrationnel pi-3. Comme pi-3 était arbitrairement choisi, ceci montre que tout irrationnel (en fait, tout réel) est bel et bien la limite d'une suite d'intervalles qui se resserrent.
CQFD.
Merci pour cette démonstration.
Chaque IN étant contenu dans IN-1, l’intersection, à l’étape N, des intervalles emboîtés est IN.
Je ne comprends donc pas qu’à l’infini, cette intersection ne soit pas encore IN.
C’est sans doute la clef du problème car si l’intersection était l’un de ces IN, on serait encore en présence d’un ensemble infini et non d’un singleton.
Pouvez-vous éclairer notre lanterne sur ce point ?
Vanleers- Digressi(f/ve)

- Nombre de messages : 4217
Date d'inscription : 15/01/2017
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
L'intersection entre deux ensembles A et B, c'est l'ensemble constitué des éléments contenus à la fois dans A et dans B.
L'intersection d'une infinité d'ensembles IN, c'est l'ensemble constitué des éléments contenus dans tous les ensembles IN, pour tous les N (et il y en a une infinité).
Dans la suite des IN, un seul élément appartient à tous ces intervalles sans exception : c'est pi-3. Voilà pourquoi l'intersection le contient comme unique élément.
https://fr.wikipedia.org/wiki/Intersection_(math%C3%A9matiques)#Intersection_d'une_famille_d'ensembles
Oui, en mathématiques, on peut faire une opération (ici, l'intersection) sur une infinité d'objets d'un coup, en un claquement de doigt.
L'intersection d'une infinité d'ensembles IN, c'est l'ensemble constitué des éléments contenus dans tous les ensembles IN, pour tous les N (et il y en a une infinité).
Dans la suite des IN, un seul élément appartient à tous ces intervalles sans exception : c'est pi-3. Voilà pourquoi l'intersection le contient comme unique élément.
https://fr.wikipedia.org/wiki/Intersection_(math%C3%A9matiques)#Intersection_d'une_famille_d'ensembles
Oui, en mathématiques, on peut faire une opération (ici, l'intersection) sur une infinité d'objets d'un coup, en un claquement de doigt.
Leonhard- Digressi(f/ve)

- Nombre de messages : 194
Date d'inscription : 03/09/2007
 Re: L'infini est-il limité ?
Re: L'infini est-il limité ?
https://www.cairn.info/revue-de-metaphysique-et-de-morale-2011-2-page-203.htmLeibniz a écrit:Non obstant mon Calcul Infinitesimal, je n’admets point de veritable nombre infini, quoyque je confesse que la multitude des choses passe tout nombre fini, ou plustôt tout nombre. […] Le Calcul infinitesimal est utile, quand il s’agit d’appliquer la Mathematique à la Physique, cependant ce n’est point par là que je pretends rendre compte de la nature des choses. Car je considere les quantités infinitesimales comme des fictions utiles.
(À Masson, 1716, GP VI, 629. .)
37Et c’est pourquoi il n’hésitera pas à moquer ceux qui, à l’instar de Fontenelle, entendaient en tirer quelques éléments métaphysiques :
38
Entre nous je crois que Mons. de Fontenelle, qui a l’esprit galant et beau, en a voulu railler, lorsqu’il a dit qu’il vouloit faire des elemens metaphysiques de nostre calcul. Pour dire le vray, je ne suis pas trop persuadé moy même, qu’il faut considerer nos infinis et infiniment petits autrement que comme des choses ideales ou comme des fictions bien fondées. Je croy qu’il n’y a point de creature au dessous de laquelle il n’y ait une infinité de creatures, cependant je ne crois point qu’il y en ait, ny même qu’il y en puisse avoir d’infiniment petites et c’est ce que je crois pouvoir demonstrer.
hks- Digressi(f/ve)

- Nombre de messages : 12518
Localisation : Hauts de Seine
Date d'inscription : 04/10/2007
Page 5 sur 9 •  1, 2, 3, 4, 5, 6, 7, 8, 9
1, 2, 3, 4, 5, 6, 7, 8, 9 
Page 5 sur 9
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum

 par hks Dim 18 Avr 2021 - 0:32
par hks Dim 18 Avr 2021 - 0:32