Prigogine , dans l'absolu
Page 1 sur 1
 Prigogine , dans l'absolu
Prigogine , dans l'absolu
bonjour
entre parenthèses je reprendrai mon autre fil plus tard
j'ai trouvé un truc plus fondamental : tenir compte du dogme de Prigogine
Prigogine développe la thèse suivante : la science classique considérait les phénomènes comme déterminés et réversibles, ce qui est en contradiction avec l'expérience courante. L'irréversibilité des phénomènes temporels caractéristique de la thermodynamique (non linéaire) réconcilie la physique avec le sens commun
source : http://fr.wikipedia.org/wiki/Ilya_Prigogine
sans pour autant utiliser la thermodynamique on peut toutefois re-écrire toute la physique classique selon un modele algebrique parametrable afin de le faire correspondre au deuxième principe de la thermodynamique
en physique classique le parametre (ou variable) temps t est considéré comme un nombre réel lequel obeit aux mêmes lois que les positions dans l'espace : il peut s'additionner selon les mêmes règles que l'addition des nombres réels
cette possibilité de la physique classique fait que dans cette mécanique les lois sont identiques que l'on considère le sens du temps allant du passé vers le futur ou l'inverse
il existe cependant une possibilité de re-écrire toutes les lois de la physique classique (sans préjuger de la validité des ces lois)
en tenant en compte le fait que ces équations different selon le sens que l'on donne au temps et cela sans même avoir besoin d'entrer dans les concepts de la thermodynamique
pour ce faire je remplace l'addition temporelle par une autre loi (qui est parametrable)
en notant * cette loi (celle-ci reste parametrable elle n'est donc pas unique mais obeit aux mêmes règles quelque soit le parametre choisit ) on obtiens la non commutativité
t_a*t_b n'est pas égal à t_b*t_a bien que l'on obtienne toujours
t_a+t_b=(t_a*t_b)+(t_b*t_a)
ici pour obtenir les mêmes valeurs de l'addition des parametres temps t utilisée dans la physique classique il faut appliquer certaines regles
ainsi donc
attention ci-dessous ici t_a et t_b ne désignent pas des variables temporelles les variables temporelles sont écrites sous la forme du produit x.u
par ailleurs l'égalitée n'est donc pas respectée lorsque t_a diffère de t_b
dans l'image que j'ai faites ce matin ci-dessous j'ai écris à tord l'égalitée x.u=...
mais c'est pour le cas particulier t_a = t_b
c'est justement grâce à cela que l'on différencie ici dans mon modèle le sens du temps
(je rappelle que ici les notations t_a et t_b ne designent pas des variables temporelles mais c'est le produit x.u qui désigne ces variables)
le symbole équivalence serait préférable (mais bon je le dit pour qu'on soit d'accord)

où cette opération est expliquée ci-dessous ->
juste ci-dessous M(a,b) désigne la moyenne arithmético-géométrique du couple (a,b)



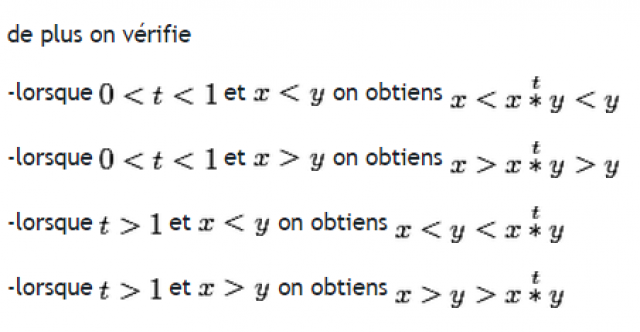

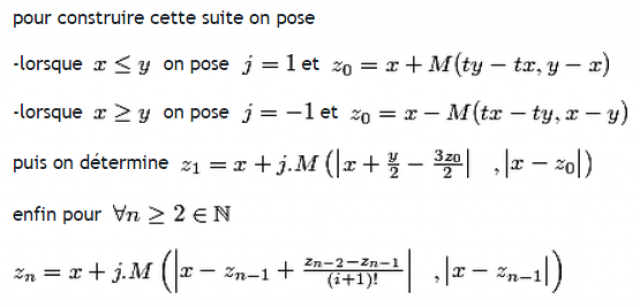
entre parenthèses je reprendrai mon autre fil plus tard
j'ai trouvé un truc plus fondamental : tenir compte du dogme de Prigogine
Prigogine développe la thèse suivante : la science classique considérait les phénomènes comme déterminés et réversibles, ce qui est en contradiction avec l'expérience courante. L'irréversibilité des phénomènes temporels caractéristique de la thermodynamique (non linéaire) réconcilie la physique avec le sens commun
source : http://fr.wikipedia.org/wiki/Ilya_Prigogine
sans pour autant utiliser la thermodynamique on peut toutefois re-écrire toute la physique classique selon un modele algebrique parametrable afin de le faire correspondre au deuxième principe de la thermodynamique
en physique classique le parametre (ou variable) temps t est considéré comme un nombre réel lequel obeit aux mêmes lois que les positions dans l'espace : il peut s'additionner selon les mêmes règles que l'addition des nombres réels
cette possibilité de la physique classique fait que dans cette mécanique les lois sont identiques que l'on considère le sens du temps allant du passé vers le futur ou l'inverse
il existe cependant une possibilité de re-écrire toutes les lois de la physique classique (sans préjuger de la validité des ces lois)
en tenant en compte le fait que ces équations different selon le sens que l'on donne au temps et cela sans même avoir besoin d'entrer dans les concepts de la thermodynamique
pour ce faire je remplace l'addition temporelle par une autre loi (qui est parametrable)
en notant * cette loi (celle-ci reste parametrable elle n'est donc pas unique mais obeit aux mêmes règles quelque soit le parametre choisit ) on obtiens la non commutativité
t_a*t_b n'est pas égal à t_b*t_a bien que l'on obtienne toujours
t_a+t_b=(t_a*t_b)+(t_b*t_a)
ici pour obtenir les mêmes valeurs de l'addition des parametres temps t utilisée dans la physique classique il faut appliquer certaines regles
ainsi donc
attention ci-dessous ici t_a et t_b ne désignent pas des variables temporelles les variables temporelles sont écrites sous la forme du produit x.u
par ailleurs l'égalitée n'est donc pas respectée lorsque t_a diffère de t_b
dans l'image que j'ai faites ce matin ci-dessous j'ai écris à tord l'égalitée x.u=...
mais c'est pour le cas particulier t_a = t_b
c'est justement grâce à cela que l'on différencie ici dans mon modèle le sens du temps
(je rappelle que ici les notations t_a et t_b ne designent pas des variables temporelles mais c'est le produit x.u qui désigne ces variables)
le symbole équivalence serait préférable (mais bon je le dit pour qu'on soit d'accord)

où cette opération est expliquée ci-dessous ->
juste ci-dessous M(a,b) désigne la moyenne arithmético-géométrique du couple (a,b)



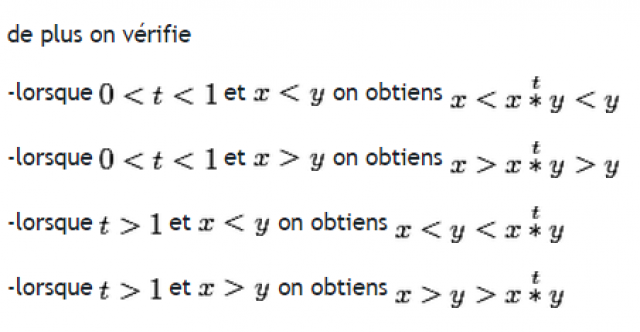

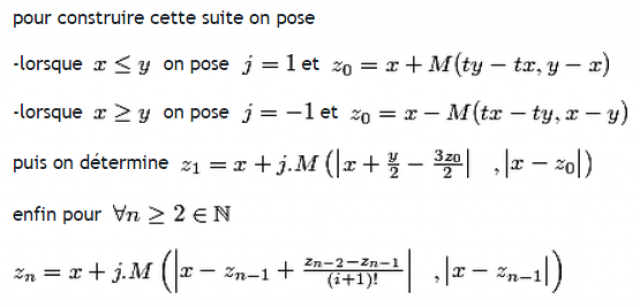

saphiraméthyste- Digressi(f/ve)

- Nombre de messages : 108
Date d'inscription : 29/11/2014
 Sujets similaires
Sujets similaires» Iraël<>Gaza ou Gaza<>Iraël, dans un sens comme dans l'autre.
» Le moi et le soi dans l'Ethique
» Le hasard dans la vie.
» Le Malaise dans la Civilisation
» gorilles dans la brume
» Le moi et le soi dans l'Ethique
» Le hasard dans la vie.
» Le Malaise dans la Civilisation
» gorilles dans la brume
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum

 par saphiraméthyste Mer 4 Fév 2015 - 8:52
par saphiraméthyste Mer 4 Fév 2015 - 8:52