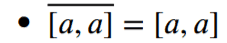Qu'est-ce qu'un segment continu ?
+3
quid
jean tardieu
Leonhard
7 participants
Page 2 sur 5
Page 2 sur 5 •  1, 2, 3, 4, 5
1, 2, 3, 4, 5 
 Re: Qu'est-ce qu'un segment continu ?
Re: Qu'est-ce qu'un segment continu ?
Leonhard a écrit:
On voit sur l'image que tout bulle autour de 1 intersecte [0, 1[. Par contre, quel que soit le x dans [0, 1[, si on "zoome" suffisamment sur x, on voit qu'il y a toujours moyen de le mettre dans une bulle qui ne contient pas 1. Ceci montre que 1 est adhérent à [0, 1[, mais qu'aucun point de [0, 1[ n'est adhérent à 1.
C'est vrai seulement avec des algébriques comme par exemple les rationnels.
Ici tu peux mettre un x' entre x et la borne sans que ce x' ne touche ni x ni la borne, ton x est un rationnel.
x n'adhère pas à 1 parce que tu peux mettre un rationnel entre lui et 1.
Il y a des points adhérents ou il n'y a pas de points adhérents ?
- Il n'y a pas de points adhérent algébriques.
- Il y a une infinité de points adhérents réels pour chaque nombre algébrique, donc tous ces points adhérents à 1 ne sont pas algébriques.
La différence algébrique entre deux points adhérents est nulle.
Mais il existe des réels qui sont différents et qui sont adhérents, les adhérents réels viennent par paquets infini, les adhérents rationnels vienne par paquets d'ensemble vide.
Dernière édition par Magni le Mar 4 Mai 2021 - 14:40, édité 1 fois
Magni- Digressi(f/ve)

- Nombre de messages : 1065
Date d'inscription : 03/05/2016
 Re: Qu'est-ce qu'un segment continu ?
Re: Qu'est-ce qu'un segment continu ?
C'est exact.Magni a écrit:Si ce que tu dis est juste alors {1} n'a aucun adhérent et les points n'adhèrent qu'aux intervalles et non aux autres points.
Non, c'est valable pour tous les réels, ce qui inclut les irrationnels, les transcendants, etc. Aucun de mes raisonnements ne présuppose que les réels dont je parle sont rationnels.Magni a écrit:Tout ce que tu dis n'est valable que pour les rationnels.
Non. {1} n'a aucun point adhérent tout court (autre que lui-même), ni à gauche, ni à droite. Je te l'ai démontré dans mon message précédent (et c'était valable pour tous les réels, pas seulement pour les rationnels), mais je constate que tu ne comprends pas les démonstrations. Je ne peux donc que te citer ces résultats venant de sources extérieures, pour que tu voies que ce ne sont pas mes opinions personnelles.Magni a écrit:Répond plutôt à cette question, s'il te plait.
{1} a-t-il oui ou non une infinité de points d'adhérents, à droite et à gauche sur le segment [0, 2] continu ?
Voici une façon de voir que {1} n'a aucun point adhérent autre que lui-même.
D'abord, on appelle adhérence d'un intervalle l'ensemble de tous les points qui sont adhérents à cet intervalle.
- Le singleton {1}, c'est l'intervalle [1, 1]. C'est un intervalle fermé, qui ne contient qu'un seul élément.
Je cite Wikipédia (ici):Wikipédia a écrit:les singletons {a} = [a, a] (fermé et non ouvert) ; - Tout intervalle fermé est égal à son adhérence.
Je cite Wikipédia (ici) :
Je cite aussi ce cours :Wikipédia a écrit:Une partie est fermée si et seulement si elle est égale à son adhérence.
La notation Ā désigne l'adhérence de A.Page 18 a écrit:A=Ā si et seulement si A est fermé. - Donc {1} est égal à son adhérence, puisque {1} est fermé.
- Donc l'ensemble de tous les points adhérents à {1}, c'est {1} lui-même.
- Donc {1} n'admet aucun point adhérent autre que 1 lui-même.
Je peux encore citer Wikipédia (ici) :
Ou ce cours (page 13) :Wikipédia a écrit:L'adhérence d'un intervalle de ℝ est l'intervalle fermé de mêmes bornes
Ou cet autre cours (page 120) :Page 13 a écrit:L’adhérence d’un intervalle borné non vide est l’intervalle fermé de mêmes extrémités.
Il découle de cette propriété que l'adhérence de l'intervalle [1, 1], c'est l'intervalle fermé de même bornes, c'est-à-dire [1, 1] lui-même. Donc, {1} est sa propre adhérence. Donc 1 est le seul point adhérent à {1}.Page 120 a écrit:L'adhérence d'un intervalle d'extrémités a et b est l'intervalle fermé [a, b].
C'est confirmé par exemple ici (page 18) :
Dans ce document, ce passage fait partie de la section 7.4 qui porte bien sur les nombres réels. Donc, dans les nombres réels, {1} ne possède aucun point adhérent (ni algébrique, ni transcendant, ni réel) autre que 1 lui-même.
Leonhard- Digressi(f/ve)

- Nombre de messages : 194
Date d'inscription : 03/09/2007
 Re: Qu'est-ce qu'un segment continu ?
Re: Qu'est-ce qu'un segment continu ?
Tout cela est beau mais je ne suis toujours pas d'accord avec toi.
L'ensemble des réels est un ensemble complet, on ne peut zoomer à aucun endroit sans trouver un réel qui est déjà là.
Dans R, il y a des réels partout en continu. Aucun endroit n'est vacant. Il n'y a aucun trou.
On prend un réel, on regarde juste à coté si il manque le point adjacent, il ne manque rien, R est complet, le point adjacent est là. Il n'y a toujours pas de trou.
Si un point quelconque de R n'avait pas un adjacent (de chaque coté), alors R ne serait pas complet, il y aurait des trous. Ce n'est pas le cas.
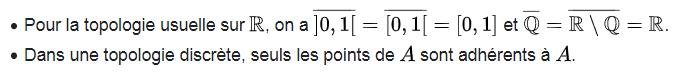
Adhérence, intérieur
L'ensemble des rationnels n'est pas égal à l'ensemble de réels.
Dans R, l'ensemble Q des rationnels n'est pas l'ensemble des Réels.
Dans R, l'ensemble des rationnels avec ses adhérents (qui ne sont pas dans Q, aucun rationnel n'adhère à un autre rationnel), est équivalent à l'ensemble des réels.
L'ensemble des réels est un ensemble complet, on ne peut zoomer à aucun endroit sans trouver un réel qui est déjà là.
Dans R, il y a des réels partout en continu. Aucun endroit n'est vacant. Il n'y a aucun trou.
On prend un réel, on regarde juste à coté si il manque le point adjacent, il ne manque rien, R est complet, le point adjacent est là. Il n'y a toujours pas de trou.
Si un point quelconque de R n'avait pas un adjacent (de chaque coté), alors R ne serait pas complet, il y aurait des trous. Ce n'est pas le cas.
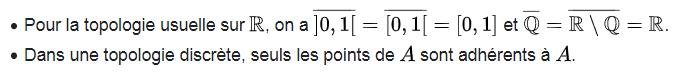
Adhérence, intérieur
L'ensemble des rationnels n'est pas égal à l'ensemble de réels.
Dans R, l'ensemble Q des rationnels n'est pas l'ensemble des Réels.
Dans R, l'ensemble des rationnels avec ses adhérents (qui ne sont pas dans Q, aucun rationnel n'adhère à un autre rationnel), est équivalent à l'ensemble des réels.
_________________
Ce que je dis n'engage que moi.

Magni- Digressi(f/ve)

- Nombre de messages : 1065
Localisation : 62100
Date d'inscription : 03/05/2016
 Re: Qu'est-ce qu'un segment continu ?
Re: Qu'est-ce qu'un segment continu ?
C'est surtout avec les maths que tu n'es pas d'accord :)Magni a écrit:Tout cela est beau mais je ne suis toujours pas d'accord avec toi.
Oui, R est complet. Et en même temps, le singleton {1} est sa propre adhérence, c'est-à-dire qu'il ne contient aucun point adhérent à gauche ni à droite. C'est démontré indubitablement par le consensus mathématique là-dessus, tel qu'on le voit dans mes précédents messages.Magni a écrit:Si un point quelconque de R n'avait pas un adjacent (de chaque coté), alors R ne serait pas complet, il y aurait des trous. Ce n'est pas le cas.
Tout ce que tu affirmes à l'encontre de cela est mathématiquement faux, inéluctablement.
Leonhard- Digressi(f/ve)

- Nombre de messages : 194
Date d'inscription : 03/09/2007
 Re: Qu'est-ce qu'un segment continu ?
Re: Qu'est-ce qu'un segment continu ?
Leonhard a écrit:le singleton {1} est sa propre adhérence, c'est-à-dire qu'il ne contient aucun point adhérent à gauche ni à droite. C'est démontré indubitablement par le consensus mathématique là-dessus, tel qu'on le voit dans mes précédents messages.
Tout ce que tu affirmes à l'encontre de cela est mathématiquement faux, inéluctablement.
Le singleton {1} est un singleton, donc il n'a pas d'adhérent dans {1} en dehors de lui même, on est d'accord.
Le singleton {1} a des adhérents dans R. Sur ce point je crois que tu n'es pas d'accord.
_________________
Ce que je dis n'engage que moi.

Magni- Digressi(f/ve)

- Nombre de messages : 1065
Localisation : 62100
Date d'inscription : 03/05/2016
 Re: Qu'est-ce qu'un segment continu ?
Re: Qu'est-ce qu'un segment continu ?
C'est surtout faux.Magni a écrit:Le singleton {1} a des adhérents dans R. Sur ce point je crois que tu n'es pas d'accord.
L'adhérence de {1}, c'est l'ensemble de tous les réels (et pas seulement ceux dans {1}) qui sont adhérents à {1}. Tout comme l'adhérence de ]0, 1[, c'est tous les réels (pas seulement ceux dans ]0, 1[) qui sont adhérents à ]0, 1[. C'est bien pour ça que l'adhérence d'un intervalle peut contenir des éléments hors de cet intervalle.
C'est écrit dans la définition de l'adhérence (ici, page 119) :
Dans cette définition, le candidat x0 est bien un réel tout court, et pas obligatoirement un réel dans A.
Je cite également ce site :
L'adhérence d'un intervalle, c'est donc bien l'ensemble de tous les réels qui sont adhérents à cet intervalle.Macformath.net a écrit:L'ensemble des réels qui adhèrent à E est noté adh E (adhérence de E) ou encore "Ē".
adh E ={x∈R : x adhère à E}
Or, l'adhérence de {1}, est lui-même. Donc l'ensemble de tous les réels adhérents à {1}, c'est {1}. Donc 1 est le seul de tous les réels qui soit adhérent à {1}. Donc 1 n'a aucun voisin de gauche ni de droite dans les réels.
Leonhard- Digressi(f/ve)

- Nombre de messages : 194
Date d'inscription : 03/09/2007
 Re: Qu'est-ce qu'un segment continu ?
Re: Qu'est-ce qu'un segment continu ?
Leonhard a écrit:[(ici, page 119) :Dans cette définition, le candidat x0 est bien un réel tout court, et pas obligatoirement un réel dans A.
Or, l'adhérence de {1}, est lui-même. Donc l'ensemble de tous les réels adhérents à {1}, c'est {1}. Donc 1 est le seul de tous les réels qui soit adhérent à {1}. Donc 1 n'a aucun voisin de gauche ni de droite dans les réels.
Corolaire de : Définition 3.13 (Adhérences)
A est une partie non vide de R
Par exemple A = [0;1[
Soit x0, un point adhérent de A, donc x0 est dans A.
Par exemple x0 = 0,5
Soit B : un intervalle ouvert non vide, de centre x0.
Quel le plus petit intervalle B possible, qui est ouvert et non vide ?
Par exemple, l'intervalle : C = ]0,25;0,75[ ; est un intervalle ouvert qui contient x0, et qui contient au moins un élément de A. Donc x0 est adhérent à A.
Mais C n'est pas le plus petit intervalle B possible, on peut faire plus petit, par exemple D = ]0,49;0,51[.
D n'est pas non plus le plus petit intervalle ouvert possible de centre x0 qui contient des adhérents de A
[x0] ça c'est un singleton, il est non vide mais c'est un intervalle fermé, donc ce n'est pas la solution.
[x0[ ça c'est un ensemble vide, ce n'est pas une solution.
]x0] ça c'est encore un ensemble vide, ce n'est pas non plus une solution.
]x0[ ça c'est encore un ensemble vide, on n'a toujours pas de solution.
Il reste quoi ?
Leonhard, pour toi y a t il une solution ? Ou diras-tu qu'il n'y a pas de plus petit intervalle ouvert, comme il n'y a pas de point le plus proche de la borne. Ai-je compris ton argument ?, sinon explique moi, et si tu as une solution dis moi laquelle.
Dans les rationnels il n'y a pas de solution, mais il y a une solution dans les réels.
Dans les réels, si x0 est dans A, il existe un intervalle ouvert minimum non vide qui contient x0.
_________________
Ce que je dis n'engage que moi.

Magni- Digressi(f/ve)

- Nombre de messages : 1065
Localisation : 62100
Date d'inscription : 03/05/2016
 Re: Qu'est-ce qu'un segment continu ?
Re: Qu'est-ce qu'un segment continu ?
Il est donc établi que 1 n'a aucun voisin de gauche ni de droite dans les réels.
Je vois que tu essaies avec vigueur de défendre l'impossible au lieu d'accepter simplement que tu te trompes.
Mais je vais quand-même te donner une preuve que c'est faux.
Je cite toujours le même cours (ici, page 117) :
Donc il n'existe pas d'intervalle ouvert minimal contenant x.
Ce passage cité précise que l'on est bel et bien dans R, et pas seulement dans les rationnels Q.
Je vois que tu essaies avec vigueur de défendre l'impossible au lieu d'accepter simplement que tu te trompes.
Il n'y en a pas.Magni a écrit:Quel le plus petit intervalle B possible, qui est ouvert et non vide ?
Ce qui est affirmé sans preuve peut être nié sans preuve.Magni a écrit:Dans les réels, si x0 est dans A, il existe un intervalle ouvert minimum non vide qui contient x0.
Mais je vais quand-même te donner une preuve que c'est faux.
Je cite toujours le même cours (ici, page 117) :
L'exemple cité montre explicitement que si un intervalle ouvert ]a, b[ contient x, alors il existe un autre intervalle ouvert contenu dans ]a, b[ et contenant x. Donc tout intervalle ouvert contenant x, contient un intervalle ouvert encore plus petit qui contient x.
Donc il n'existe pas d'intervalle ouvert minimal contenant x.
Ce passage cité précise que l'on est bel et bien dans R, et pas seulement dans les rationnels Q.
Leonhard- Digressi(f/ve)

- Nombre de messages : 194
Date d'inscription : 03/09/2007
 Re: Qu'est-ce qu'un segment continu ?
Re: Qu'est-ce qu'un segment continu ?
Intuitivement, étant plutôt de l'avis de Magni, j'énonce ci-dessous une petite démonstration qui à mon avis va dans ce sens.
Si je ne me trompe pas, le "Lemme de Zorn" semble confirmer cette façon de voir :
https://www.normalesup.org/~rpeyre/pro/popul/zorn.pdf
Considérons deux réels « a » et « b » différents {a <> b}. L’ensemble des nombres réels étant un ensemble ordonné, on a alors soit « a » inférieur strictement à « b », soit l’inverse. Considérons que l’on soit dans le cas {a < b}. La distance entre « a » et « b » est positive et non nulle {(b – a) > 0}. Entre deux nombres réels distincts quelconques, il y a une infinité de nombres réels.
Soit F l’ensemble des nombres réels compris entre « a » à « b » et les incluant (intervalle fermé). On note F = [a ; b] cet ensemble qui est un ensemble ordonné. Cet ensemble a un élément maximum qui est le plus grand élément de cet ensemble infini de nombres et qui est sa borne supérieure « b ». « b » est l’extrémité de cet ensemble ordonné de nombres réels. Enlevons le nombre et élément « b » de cet ensemble qui est aussi son extrémité. Nous obtenons un ensemble O que l’on note O = [a ; b[. On nous dit alors que ce nouvel ensemble ordonné ainsi obtenu n’a plus d’extrémité. En effet, cet ensemble auquel on a enlevé un seul élément n’a plus d’élément maximum plus grand que les autres.
Pourquoi ? Parce-que dans cet ensemble, qui était déjà infini avant le retrait du plus grand de ses éléments, si l’on pose un plus grand élément « m », {a <= m < b} tel qu’il n’existe pas d’élément « m’ » tel que {m < m’ < b}, c’est-à-dire un élément qui pourrait s’intercaler entre « m » et « b » tout en étant différent de ceux-ci, on trouvera toujours au moins « m’ » tel que {m’ = (m+b) / 2}. « m » et « b » étant différents on trouvera toujours une infinité de nombre réels éléments de O entre « m » et « b » et {m’ = (m+b) / 2} sera toujours une solution, à l’infini de {m < m’ < b}. On trouvera donc toujours un plus grand élément que celui que l’on pourrait poser comme le plus grand élément.
Question : Est-ce à dire que l’ensemble O = [a ; b[, alors qu’il est complètement ordonné et qui est l’ensemble F = [a ; b] auquel on a seulement ôté l’élément maximum, extrémité de ce dernier, n’a plus d’extrémité ? En effet, quelle différence fondamentale y a-t-il entre un ensemble complètement ordonné d’un nombre infini d’éléments, et ce même ensemble infini auquel on a enlevé seulement un élément qui est à son extrémité ?
On pourrait donc aussi raisonner comme cela :
Quelques soit « p » l’élément appartenant à l’ensemble O = [a ; b[, il vérifie {p < b}. Tous les éléments « p » de O précèdent « b ». De manière générale, dans l’ensemble totalement ordonné des nombres réels, quelques soit « r » appartenant à cet ensemble, les autres éléments et nombre différents de « r », soit le précèdent, soit le suivent. Tout nombre réel a donc une infinité de précédents et une infinité de suivants. De plus, tous les précédents et les suivants sont différents les uns des autres. Or, si l’on prend deux nombres précédents d’un nombre quelconque « r », ils sont différents et l’un donc précède l’autre.
Donc, étant donné deux nombres quelconques parmi l’ensemble des nombres précédents du nombre réel « r », l’un précède toujours « r » de manière plus proche que le second. Dans l’ensemble infini qu’est l’ensemble des nombres précédents de « r », il ne peut donc exister qu’un seul précédent plus proche de « r ». En effet, s’il en existait plus d’un, les deux précédents devraient être égaux.
De plus, cet unique précédent existe. En effet, tous les précédents de « r » entretiennent une certaine proximité avec « r », pour chacun différente.
Il découle de ceci que O = [a ; b[ qui est l’ensemble des précédents de « b » supérieurs ou égal à « a », comprend un tel précédent plus grand que tous les autres et qui est celui le plus proche de « b ». En d’autres termes, O = [a ; b[ comprend un élément maximum qui est l’élément immédiatement inférieur à « b ».
Si je ne me trompe pas, le "Lemme de Zorn" semble confirmer cette façon de voir :
https://www.normalesup.org/~rpeyre/pro/popul/zorn.pdf
Considérons deux réels « a » et « b » différents {a <> b}. L’ensemble des nombres réels étant un ensemble ordonné, on a alors soit « a » inférieur strictement à « b », soit l’inverse. Considérons que l’on soit dans le cas {a < b}. La distance entre « a » et « b » est positive et non nulle {(b – a) > 0}. Entre deux nombres réels distincts quelconques, il y a une infinité de nombres réels.
Soit F l’ensemble des nombres réels compris entre « a » à « b » et les incluant (intervalle fermé). On note F = [a ; b] cet ensemble qui est un ensemble ordonné. Cet ensemble a un élément maximum qui est le plus grand élément de cet ensemble infini de nombres et qui est sa borne supérieure « b ». « b » est l’extrémité de cet ensemble ordonné de nombres réels. Enlevons le nombre et élément « b » de cet ensemble qui est aussi son extrémité. Nous obtenons un ensemble O que l’on note O = [a ; b[. On nous dit alors que ce nouvel ensemble ordonné ainsi obtenu n’a plus d’extrémité. En effet, cet ensemble auquel on a enlevé un seul élément n’a plus d’élément maximum plus grand que les autres.
Pourquoi ? Parce-que dans cet ensemble, qui était déjà infini avant le retrait du plus grand de ses éléments, si l’on pose un plus grand élément « m », {a <= m < b} tel qu’il n’existe pas d’élément « m’ » tel que {m < m’ < b}, c’est-à-dire un élément qui pourrait s’intercaler entre « m » et « b » tout en étant différent de ceux-ci, on trouvera toujours au moins « m’ » tel que {m’ = (m+b) / 2}. « m » et « b » étant différents on trouvera toujours une infinité de nombre réels éléments de O entre « m » et « b » et {m’ = (m+b) / 2} sera toujours une solution, à l’infini de {m < m’ < b}. On trouvera donc toujours un plus grand élément que celui que l’on pourrait poser comme le plus grand élément.
Question : Est-ce à dire que l’ensemble O = [a ; b[, alors qu’il est complètement ordonné et qui est l’ensemble F = [a ; b] auquel on a seulement ôté l’élément maximum, extrémité de ce dernier, n’a plus d’extrémité ? En effet, quelle différence fondamentale y a-t-il entre un ensemble complètement ordonné d’un nombre infini d’éléments, et ce même ensemble infini auquel on a enlevé seulement un élément qui est à son extrémité ?
On pourrait donc aussi raisonner comme cela :
Quelques soit « p » l’élément appartenant à l’ensemble O = [a ; b[, il vérifie {p < b}. Tous les éléments « p » de O précèdent « b ». De manière générale, dans l’ensemble totalement ordonné des nombres réels, quelques soit « r » appartenant à cet ensemble, les autres éléments et nombre différents de « r », soit le précèdent, soit le suivent. Tout nombre réel a donc une infinité de précédents et une infinité de suivants. De plus, tous les précédents et les suivants sont différents les uns des autres. Or, si l’on prend deux nombres précédents d’un nombre quelconque « r », ils sont différents et l’un donc précède l’autre.
Donc, étant donné deux nombres quelconques parmi l’ensemble des nombres précédents du nombre réel « r », l’un précède toujours « r » de manière plus proche que le second. Dans l’ensemble infini qu’est l’ensemble des nombres précédents de « r », il ne peut donc exister qu’un seul précédent plus proche de « r ». En effet, s’il en existait plus d’un, les deux précédents devraient être égaux.
De plus, cet unique précédent existe. En effet, tous les précédents de « r » entretiennent une certaine proximité avec « r », pour chacun différente.
Il découle de ceci que O = [a ; b[ qui est l’ensemble des précédents de « b » supérieurs ou égal à « a », comprend un tel précédent plus grand que tous les autres et qui est celui le plus proche de « b ». En d’autres termes, O = [a ; b[ comprend un élément maximum qui est l’élément immédiatement inférieur à « b ».

quid- Digressi(f/ve)

- Nombre de messages : 1080
Date d'inscription : 04/08/2012
 Re: Qu'est-ce qu'un segment continu ?
Re: Qu'est-ce qu'un segment continu ?
quid a écrit: O = [a ; b[ qui est l’ensemble des précédents de « b » supérieurs ou égal à « a », comprend un tel précédent plus grand que tous les autres et qui est celui le plus proche de « b ». En d’autres termes, O = [a ; b[ comprend un élément maximum qui est l’élément immédiatement inférieur à « b ».
C'est vrai dans le continu. R est un ensemble continu, donc c'est vrai dans R.
Dans le dénombrable, parmi les rationnels, il n'y a pas de nombre le plus proche de b, on peut toujours mettre un algébrique moyen entre deux nombres qui ont une différence avec une partie mesurable. C'est ce qui caractérise le dénombrable et on a étudié le problème dans les arguments de Zénon. Appliquer les caractéristiques du dénombrable sur tous les réels est une erreur car tous les réels ne sont pas dénombrables.
Dans l'indénombrable qui a la puissance du continu, quand on est dans un ensemble complet qui permet la continuité en tout point, quand on est dans un environnement mathématique créé sur mesure pour dépasser le problème des arguments de Zénon, alors on ne peut pas toujours ajouter un nombre avant la borne.
R est complet dans le continu et il est nécessaire qu'il y ait un dernier élément avant la borne, sinon on retombe sur le problème de l'arguments de Zénon et dans le dénombrable.
La différence entre b et son précédent adjacent n'est pas mesurable.
On peut en partie connaître Pi et Pi est partiellement inconnaissable. Pi vaut presque 3,14; la parie inconnue de Pi vaut 0,(31 trillons de zéro)+quelque chose d'inconnu. Cette partie va rapetisser mais elle ne disparaitra pas, cela ne sera jamais exactement zéro.
Mais la partie non connu de Pi est très petite par rapport a la partie connue.
La différence entre b et son précédent adjacent n'a aucune partie connaissable, ce nombre est totalement inconnaissable.
Et donc, le prédécesseur de b est inférieur ou égal à b et on ne peut pas en savoir plus, la trichotomie ne s'applique pas à deux nombres dont la différence est totalement inconnue.
_________________
Ce que je dis n'engage que moi.

Magni- Digressi(f/ve)

- Nombre de messages : 1065
Localisation : 62100
Date d'inscription : 03/05/2016
 Re: Qu'est-ce qu'un segment continu ?
Re: Qu'est-ce qu'un segment continu ?
La démonstration qui précède la conclusion que tu as cité vaut pour les ensembles ordonnés, pas forcément continus. En tout cas elle vaut pour les nombres rationnels qui sont denses sur le réel.Magni a écrit:quid a écrit: O = [a ; b[ qui est l’ensemble des précédents de « b » supérieurs ou égal à « a », comprend un tel précédent plus grand que tous les autres et qui est celui le plus proche de « b ». En d’autres termes, O = [a ; b[ comprend un élément maximum qui est l’élément immédiatement inférieur à « b ».
C'est vrai dans le continu. R est un ensemble continu, donc c'est vrai dans R.
Dans le dénombrable, parmi les rationnels, il n'y a pas de nombre le plus proche de b, on peut toujours mettre un algébrique moyen entre deux nombres qui ont une différence avec une partie mesurable. C'est ce qui caractérise le dénombrable et on a étudié le problème dans les arguments de Zénon. Appliquer les caractéristiques du dénombrable sur tous les réels est une erreur car tous les réels ne sont pas dénombrables.

quid- Digressi(f/ve)

- Nombre de messages : 1080
Date d'inscription : 04/08/2012
 Re: Qu'est-ce qu'un segment continu ?
Re: Qu'est-ce qu'un segment continu ?
Tout argument qui s'opposerait au résultat mathématique établi suivant est nécessairement mathématiquement invalide :
Cité de ce document.Page 2 a écrit:L'intervalle [0, 1[ admet 0 pour plus petit élément, mais N'A PAS de plus grand élément.
Dernière édition par Leonhard le Jeu 6 Mai 2021 - 16:17, édité 3 fois
Leonhard- Digressi(f/ve)

- Nombre de messages : 194
Date d'inscription : 03/09/2007
 Re: Qu'est-ce qu'un segment continu ?
Re: Qu'est-ce qu'un segment continu ?
C'est mathématiquement faux. La trichotomie s'applique à tous les réels, quels qu'ils soient.Magni a écrit:la trichotomie ne s'applique pas à deux nombres dont la différence est totalement inconnue.
Je cite ce document, page 3 :
Page 3 a écrit:P6 (trichotomie) Pour tous x, y ∈ R,
soit x < y, soit x = y, soit x > y,
Je cite aussi ce document, page 8 :
Page 8 a écrit:A10 Quels que soient x et y ∈ R, une et une seule des trois possibilités
suivantes est réalisée : x > y, x = y, x < y.
Leonhard- Digressi(f/ve)

- Nombre de messages : 194
Date d'inscription : 03/09/2007
 Re: Qu'est-ce qu'un segment continu ?
Re: Qu'est-ce qu'un segment continu ?
La limite du plus grand nombre strictement avant une borne est la borne.
Mais je viens de dire que ce nombre est strictement avant la borne, donc ce n'est pas la borne.
Ce n'est pas le nombre qui est la borne, c'est la limite qui est la borne !
Tous les points qui sont strictement avant la borne ne sont pas la borne.
Au niveau algébrique, pour tout x élément de R, la limite du x le plus proche de Pi sans être Pi est Pi. C'est la limite qui est Pi.
On a un point qui n'est pas Pi, mais dont la valeur algébrique est Pi.
Ce nombre est il plus petit que Pi ou égal à Pi. Ce nombre existe t il ?
Si tu te place dans le non continu, dans Q la limite du x le plus proche de Pi sans être Pi n'existe pas. Il y a discontinuité dans le non continu, évidemment.
Donc, s'il y a une limite, il y a du continu, et le plus petit nombre avant zéro qui n'est pas zéro existe.
Quand le plus petit nombre avant zéro qui n'est pas zéro n'existe pas, on a une discontinuité.
Pour avoir une limite, il faut que le nombre non nul le plus petit existe ! S'il n'existe pas, pas de limite, pas de continu, on n'est pas dans les réels.
Dans R la limite du x le plus grand avant Pi sans être Pi existe, et même si sa valeur algébrique est la même que la valeur algébrique de Pi, sa valeur complète n'est pas la même que la valeur complète de Pi, car il n'est pas Pi.
Ce nombre est plus petit ou égal à Pi, c'est la seule chose que tu sais avec la relation algébrique de la trichotomie.
Peut être qu'il est égal à Pi, peut être qu'il est plus petit, la trichotomie le sait mais toi, comment peux tu le savoir et appliquer la trochotomie ?
Dire que ce nombre n'existe pas parce que ce nombre ne peut pas être un rationnel n'est pas une réponse valable dans les Réels au complet.
Si tu veux trancher, tu dois dire que ces nombres sont algébriquement égaux donc tu ne peux pas mettre un algébrique entre les deux, mais analytiquement, tu sais que ce sont deux réels différents, car ce qui est strictement avant la borne n'est pas la borne.
Mais je viens de dire que ce nombre est strictement avant la borne, donc ce n'est pas la borne.
Ce n'est pas le nombre qui est la borne, c'est la limite qui est la borne !
Tous les points qui sont strictement avant la borne ne sont pas la borne.
Au niveau algébrique, pour tout x élément de R, la limite du x le plus proche de Pi sans être Pi est Pi. C'est la limite qui est Pi.
On a un point qui n'est pas Pi, mais dont la valeur algébrique est Pi.
Ce nombre est il plus petit que Pi ou égal à Pi. Ce nombre existe t il ?
Si tu te place dans le non continu, dans Q la limite du x le plus proche de Pi sans être Pi n'existe pas. Il y a discontinuité dans le non continu, évidemment.
Donc, s'il y a une limite, il y a du continu, et le plus petit nombre avant zéro qui n'est pas zéro existe.
Quand le plus petit nombre avant zéro qui n'est pas zéro n'existe pas, on a une discontinuité.
Pour avoir une limite, il faut que le nombre non nul le plus petit existe ! S'il n'existe pas, pas de limite, pas de continu, on n'est pas dans les réels.
Dans R la limite du x le plus grand avant Pi sans être Pi existe, et même si sa valeur algébrique est la même que la valeur algébrique de Pi, sa valeur complète n'est pas la même que la valeur complète de Pi, car il n'est pas Pi.
Ce nombre est plus petit ou égal à Pi, c'est la seule chose que tu sais avec la relation algébrique de la trichotomie.
Peut être qu'il est égal à Pi, peut être qu'il est plus petit, la trichotomie le sait mais toi, comment peux tu le savoir et appliquer la trochotomie ?
Dire que ce nombre n'existe pas parce que ce nombre ne peut pas être un rationnel n'est pas une réponse valable dans les Réels au complet.
Si tu veux trancher, tu dois dire que ces nombres sont algébriquement égaux donc tu ne peux pas mettre un algébrique entre les deux, mais analytiquement, tu sais que ce sont deux réels différents, car ce qui est strictement avant la borne n'est pas la borne.
_________________
Ce que je dis n'engage que moi.

Magni- Digressi(f/ve)

- Nombre de messages : 1065
Localisation : 62100
Date d'inscription : 03/05/2016
 Re: Qu'est-ce qu'un segment continu ?
Re: Qu'est-ce qu'un segment continu ?
Attention : la limite du nombre le plus proche de x sans être x, n'est pas le nombre le plus proche de x sans être x.
Le nombre est avant x, la limite est x.
Dire "il n'y a pas de limite du nombre le plus proche de x avant x" c'est comme dire " il y a discontinuité en x". Donc il n'y a pas de nombre proche de x dans l'absolu, et il n'y a pas de nombre le plus proche de x. C'est le cas de la discontinuité.
Dire, "la limite du nombre le plus proche de x sans être x existe et est x" c'est comme dire, "le nombre le plus proche de x sans être x existe, il y a continuité en x".
Si le nombre le plus proche de x sans être x n'existe pas, il n'y a pas de limite en x.
Quand il y a une limite en x, le nombre le plus proche x sans être x existe.
C'est tout.
Le nombre est avant x, la limite est x.
Dire "il n'y a pas de limite du nombre le plus proche de x avant x" c'est comme dire " il y a discontinuité en x". Donc il n'y a pas de nombre proche de x dans l'absolu, et il n'y a pas de nombre le plus proche de x. C'est le cas de la discontinuité.
Dire, "la limite du nombre le plus proche de x sans être x existe et est x" c'est comme dire, "le nombre le plus proche de x sans être x existe, il y a continuité en x".
Si le nombre le plus proche de x sans être x n'existe pas, il n'y a pas de limite en x.
Quand il y a une limite en x, le nombre le plus proche x sans être x existe.
C'est tout.
_________________
Ce que je dis n'engage que moi.

Magni- Digressi(f/ve)

- Nombre de messages : 1065
Localisation : 62100
Date d'inscription : 03/05/2016
 Re: Qu'est-ce qu'un segment continu ?
Re: Qu'est-ce qu'un segment continu ?
La "limite d'un nombre", ça ne veut rien dire en maths. On parle de limite d'une suite ou d'une fonction, pas d'un nombre.Magni a écrit:Attention : la limite du nombre le plus proche de x sans être x,
Donc ce que tu dis n'a aucun sens mathématique.
Leonhard- Digressi(f/ve)

- Nombre de messages : 194
Date d'inscription : 03/09/2007
 Re: Qu'est-ce qu'un segment continu ?
Re: Qu'est-ce qu'un segment continu ?
"Le nombre le plus proche de x sans être x" est une fonction.
Cette phrase défini entièrement une fonction et sa limite.
C'est un peu comme :
Soit B : un intervalle ouvert non vide, de centre x.
Quel est le plus petit intervalle B possible, qui est ouvert et non vide ?
Par exemple, l'intervalle : C = ]0,25;0,75[ ; est un intervalle ouvert qui contient x, et qui contient au moins un élément de A. Donc x est adhérent à A.
Mais C n'est pas le plus petit intervalle B possible, on peut faire plus petit, par exemple D = ]0,49;0,51[.
D n'est pas non plus le plus petit intervalle ouvert possible de centre x qui contient des adhérents de A
Le plus petit intervalle ouvert est x avec ses deux adjacents.
soit (x-a) le plus grand réel avant x; et (x+a) le plus petit réel après x.
Voici le plus petit intervalle ouvert centré sur x dans les réels : B = ]x-a;x;x+a[ = [x]
C'est aussi un singleton, car les bornes sont exclues, mais c'est aussi un intervalle ouvert.
Et c'est impossible dans les rationnels, et c'est parce que c'est possible dans les réels que les réels sont différents des rationnels et sont pourvus de l'attribut de la continuité et arrivent jusqu'au contact du poteau.
Seuls les rationnels restent indéfiniment à une certaine distance non nulle du poteau.
Je sais , j'ai parlé de la cardinalité d'un nombre et tu n'as jamais vu ça dans tes cours, mais j'ai défini ce que c'est et ma définition est valide.
J'ai aussi parlé d'adhérence entre nombres et tu n'as pas d'exemple dans Wikipedia mais c'est encore correct. Si un point peut adhérer à un segment constitué de points, il peut aussi adhérer au dernier point du segment.
Et on peut définir verbalement une fonction de transformation d'un segment en point comme de tout x en un seul x, on peut raconter une histoire de course a la tortue en faisant des phrases d'analyse de fonction, c'est valide, on n'est pas obliger de dire le mot "fonction", il faut seulement décrire la fonction.
Cette phrase défini entièrement une fonction et sa limite.
C'est un peu comme :
Soit B : un intervalle ouvert non vide, de centre x.
Quel est le plus petit intervalle B possible, qui est ouvert et non vide ?
Par exemple, l'intervalle : C = ]0,25;0,75[ ; est un intervalle ouvert qui contient x, et qui contient au moins un élément de A. Donc x est adhérent à A.
Mais C n'est pas le plus petit intervalle B possible, on peut faire plus petit, par exemple D = ]0,49;0,51[.
D n'est pas non plus le plus petit intervalle ouvert possible de centre x qui contient des adhérents de A
Le plus petit intervalle ouvert est x avec ses deux adjacents.
soit (x-a) le plus grand réel avant x; et (x+a) le plus petit réel après x.
Voici le plus petit intervalle ouvert centré sur x dans les réels : B = ]x-a;x;x+a[ = [x]
C'est aussi un singleton, car les bornes sont exclues, mais c'est aussi un intervalle ouvert.
Et c'est impossible dans les rationnels, et c'est parce que c'est possible dans les réels que les réels sont différents des rationnels et sont pourvus de l'attribut de la continuité et arrivent jusqu'au contact du poteau.
Seuls les rationnels restent indéfiniment à une certaine distance non nulle du poteau.
Je sais , j'ai parlé de la cardinalité d'un nombre et tu n'as jamais vu ça dans tes cours, mais j'ai défini ce que c'est et ma définition est valide.
J'ai aussi parlé d'adhérence entre nombres et tu n'as pas d'exemple dans Wikipedia mais c'est encore correct. Si un point peut adhérer à un segment constitué de points, il peut aussi adhérer au dernier point du segment.
Et on peut définir verbalement une fonction de transformation d'un segment en point comme de tout x en un seul x, on peut raconter une histoire de course a la tortue en faisant des phrases d'analyse de fonction, c'est valide, on n'est pas obliger de dire le mot "fonction", il faut seulement décrire la fonction.
_________________
Ce que je dis n'engage que moi.

Magni- Digressi(f/ve)

- Nombre de messages : 1065
Localisation : 62100
Date d'inscription : 03/05/2016
 Re: Qu'est-ce qu'un segment continu ?
Re: Qu'est-ce qu'un segment continu ?
Il n'y a pas de plus grand élément avant un nombre.Magni a écrit:soit (x-a) le plus grand réel avant x;
Extrait de ce document :
Page 2 a écrit:L'intervalle [0, 1[ admet 0 pour plus petit élément, mais N'A PAS de plus grand élément.
Leonhard- Digressi(f/ve)

- Nombre de messages : 194
Date d'inscription : 03/09/2007
 Re: Qu'est-ce qu'un segment continu ?
Re: Qu'est-ce qu'un segment continu ?
Leonhard a écrit:La "limite d'un nombre", ça ne veut rien dire en maths. On parle de limite d'une suite ou d'une fonction, pas d'un nombre.Magni a écrit:Attention : la limite du nombre le plus proche de x sans être x,
Donc ce que tu dis n'a aucun sens mathématique.
Ce n'est pas la limite d'un nombre,
C'est la limite DU nombre le plus proche de x sans être x parmi tous les nombres réels.
C'est la limite de la fonction de raccourcissement à l'infini d'un segment avant x jusqu’à ce que ce segment soit réduit à la taille non nulle d'un singleton qui n'est pas x.
Et attention :
La limite de "le dernier nombre avant x" qui est x,
n'est pas
"le dernier nombre avant x" car le dernier nombre avant x n'est pas x.
_________________
Ce que je dis n'engage que moi.

Magni- Digressi(f/ve)

- Nombre de messages : 1065
Localisation : 62100
Date d'inscription : 03/05/2016
 Re: Qu'est-ce qu'un segment continu ?
Re: Qu'est-ce qu'un segment continu ?
Je continue dans le sens de Magni.
Soit l'intervalle fermé F = [0 ; b]
La longueur de F est (b - 0) = b, notons la Lg(F) = b
Soit l'intervalle ouvert O = [0 ; b[ on a donc ∀p ∈ O, p < b
Il en résulte que Lg(O) < b
Soit l'intervalle de type singleton S = {b} = [b ; b]
Lg(S) = (b - b) = 0
F = [0 ; b] = [0 ; b[ ∪ [b ; b] = O ∪ S avec O ∩ S = ∅
On devrait donc avoir Lg(F) = Lg(O) + Lg(S)
Puisque Lg(S) = 0 alors Lg(F) = Lg(O) et donc Lg(F) - Lg(O) = 0
Mais Lg(F) = b et Lg(O) < b donc Lg(F) - Lg(O) > 0, ce qui est contradictoire
O = [0 ; b[ doit donc permettre d'avoir, et donc d'inclure, un élément {m} ≠ {b} et avant {b} tel que m = b, afin que Lg(O) puisse être égal à b.
Cet élément {m} est un plus grand élément de O car avec une différence numérique de 0 avec {b}, ce qui en fait la distance la plus proche possible de {b}. De plus, l'ensemble F étant ordonné, {b} n'a qu'un seul prédécesseur de la sorte, ce qui fait de {m} l'unique plus grand prédécesseur de {b}.
Soit l'intervalle fermé F = [0 ; b]
La longueur de F est (b - 0) = b, notons la Lg(F) = b
Soit l'intervalle ouvert O = [0 ; b[ on a donc ∀p ∈ O, p < b
Il en résulte que Lg(O) < b
Soit l'intervalle de type singleton S = {b} = [b ; b]
Lg(S) = (b - b) = 0
F = [0 ; b] = [0 ; b[ ∪ [b ; b] = O ∪ S avec O ∩ S = ∅
On devrait donc avoir Lg(F) = Lg(O) + Lg(S)
Puisque Lg(S) = 0 alors Lg(F) = Lg(O) et donc Lg(F) - Lg(O) = 0
Mais Lg(F) = b et Lg(O) < b donc Lg(F) - Lg(O) > 0, ce qui est contradictoire
O = [0 ; b[ doit donc permettre d'avoir, et donc d'inclure, un élément {m} ≠ {b} et avant {b} tel que m = b, afin que Lg(O) puisse être égal à b.
Cet élément {m} est un plus grand élément de O car avec une différence numérique de 0 avec {b}, ce qui en fait la distance la plus proche possible de {b}. De plus, l'ensemble F étant ordonné, {b} n'a qu'un seul prédécesseur de la sorte, ce qui fait de {m} l'unique plus grand prédécesseur de {b}.

quid- Digressi(f/ve)

- Nombre de messages : 1080
Date d'inscription : 04/08/2012
 Re: Qu'est-ce qu'un segment continu ?
Re: Qu'est-ce qu'un segment continu ?
Leonhard a écrit:Il n'y a pas de plus grand élément avant un nombre.Magni a écrit:soit (x-a) le plus grand réel avant x;
Extrait de ce document :Page 2 a écrit:L'intervalle [0, 1[ admet 0 pour plus petit élément, mais N'A PAS de plus grand élément.
Je ne suis pas d'accord.
S'il n'y a rien immédiatement à gauche en 1 alors le segment n'est pas continu.
Si on est dans les réels, il doit y avoir continuité jusqu'à la borne.

Limite à droite
Le point qui est à droite de x0, en limite de x0, sans être x0 ... est x0+
x0+ existe, c'est la continuité des réels qui l'implique.
Les réels sont continu partout, même juste à coté de la borne.
_________________
Ce que je dis n'engage que moi.

Magni- Digressi(f/ve)

- Nombre de messages : 1065
Localisation : 62100
Date d'inscription : 03/05/2016
 Re: Qu'est-ce qu'un segment continu ?
Re: Qu'est-ce qu'un segment continu ?
Cette implication est fausse, puisque [0, 1[ n'a pas de plus grand élément (c'est un fait mathématique), et en même temps la droite réelle est continue (c'est aussi un fait). C'est juste que tu n'arrives pas à faire cohabiter ces deux faits à cause d'une compréhension intuitive et fausse de la continuité.Magni a écrit:Leonhard a écrit:Il n'y a pas de plus grand élément avant un nombre.Magni a écrit:soit (x-a) le plus grand réel avant x;
Extrait de ce document :Page 2 a écrit:L'intervalle [0, 1[ admet 0 pour plus petit élément, mais N'A PAS de plus grand élément.
Je ne suis pas d'accord.
S'il n'y a rien immédiatement à gauche en 1 alors le segment n'est pas continu.
Tu ne trouveras aucune référence mathématique disant que [a, b[ possède un maximum ou un plus grand élément.
Quant à la notation x0+ des limites à droite, le + ne sert qu'à exprimer le fait que la variable x tende vers x0 en restant supérieure à x0, et d'autres conventions d'écriture existent avec le symbole > au lieu de l'exposant +, comme
 . En aucun cas, x0+ ne désigne un nombre réel différent de x0. Dans la définition même de la limite à droite, d'ailleurs, on voit que la valeur cible de la variable x, c'est bien x0, et non un inexistant nombre réel "juste à droite de x0".
. En aucun cas, x0+ ne désigne un nombre réel différent de x0. Dans la définition même de la limite à droite, d'ailleurs, on voit que la valeur cible de la variable x, c'est bien x0, et non un inexistant nombre réel "juste à droite de x0".https://fr.wikipedia.org/wiki/Limite_(math%C3%A9matiques)#Limite_%C3%A0_gauche_ou_%C3%A0_droite
Tu as simplement pris un abus de notation à la lettre, au lieu de comprendre sa signification réelle.
Leonhard- Digressi(f/ve)

- Nombre de messages : 194
Date d'inscription : 03/09/2007
 Re: Qu'est-ce qu'un segment continu ?
Re: Qu'est-ce qu'un segment continu ?
Intéressante tentative.quid a écrit:Je continue dans le sens de Magni.
Soit l'intervalle fermé F = [0 ; b]
La longueur de F est (b - 0) = b, notons la Lg(F) = b
Soit l'intervalle ouvert O = [0 ; b[ on a donc ∀p ∈ O, p < b
Il en résulte que Lg(O) < b
Soit l'intervalle de type singleton S = {b} = [b ; b]
Lg(S) = (b - b) = 0
F = [0 ; b] = [0 ; b[ ∪ [b ; b] = O ∪ S avec O ∩ S = ∅
On devrait donc avoir Lg(F) = Lg(O) + Lg(S)
Puisque Lg(S) = 0 alors Lg(F) = Lg(O) et donc Lg(F) - Lg(O) = 0
Mais Lg(F) = b et Lg(O) < b donc Lg(F) - Lg(O) > 0, ce qui est contradictoire
O = [0 ; b[ doit donc permettre d'avoir, et donc d'inclure, un élément {m} ≠ {b} et avant {b} tel que m = b, afin que Lg(O) puisse être égal à b.
Cet élément {m} est un plus grand élément de O car avec une différence numérique de 0 avec {b}, ce qui en fait la distance la plus proche possible de {b}. De plus, l'ensemble F étant ordonné, {b} n'a qu'un seul prédécesseur de la sorte, ce qui fait de {m} l'unique plus grand prédécesseur de {b}.
Tu essaies d'invoquer un élément m tel que {m} ≠ {b} et, en même temps, m = b. Malheureusement cet élément n'existe pas.
En effet, {m} ≠ {b} implique que m ≠ b (c'est écrit ici, par exemple).
Or, tu exiges en même temps que m = b.
C'est logiquement impossible.
Donc ton élément m n'existe tout simplement pas.
Si m=b, alors m est hors de [0, b[ et n'est pas le dernier élément de cet intervalle.
Et si m est dans [0, b[, alors cet intervalle serait [0, m], mais m<b et l'intervalle n'est alors pas de longueur b.
En fait, la contradiction que tu as obtenue montre seulement que l'hypothèse soulignée est fausse. En effet, la longueur de [0, b[ est b. Et avec cela, aucune contradiction, aucun besoin d'inventer des nombres qui n'existent pas.
De façon général, un intervalle de bornes a et b, qu'il soit ouvert, fermé ou semi-ouvert, est de longueur fixe b-a.
https://www.ukonline.be/cours/math/basehigher-summary/chapitre3-1
Dernière édition par Leonhard le Ven 7 Mai 2021 - 10:45, édité 2 fois (Raison : l)
Leonhard- Digressi(f/ve)

- Nombre de messages : 194
Date d'inscription : 03/09/2007
 Re: Qu'est-ce qu'un segment continu ?
Re: Qu'est-ce qu'un segment continu ?
Très bon exemple !
Limite à droite et à gauche
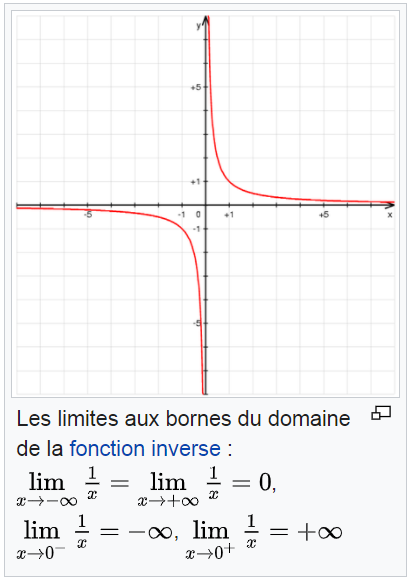
C'est le cas dont j'ai déjà parlé, et je constate sans beaucoup d'étonnement que d'autres y avait déjà pensé avant moi.
La limite de la fonction à droite et à gauche de zéro ne pointe pas vers la même valeur.
Et ici, on a besoin de 0- et 0+
x=1/0 n'existe pas dans les réels
1/0+= limite à l'infini
1/0-= limite à moins l'infini
0+ et 0- sont différents de zéro, le résultat de 1/0+ ou 1/0- existent, 1/0 n'existe pas dans les réels
Il y a continuité entre 0- ; 0 et 0+
Attention, la limite de la fonction n'est pas le produit de la fonction à la limite :
Limite de 1/x en 0+ = l'infini
1/0+ = limite à l'infini
Limite à droite et à gauche

C'est le cas dont j'ai déjà parlé, et je constate sans beaucoup d'étonnement que d'autres y avait déjà pensé avant moi.
La limite de la fonction à droite et à gauche de zéro ne pointe pas vers la même valeur.
Et ici, on a besoin de 0- et 0+
x=1/0 n'existe pas dans les réels
1/0+= limite à l'infini
1/0-= limite à moins l'infini
0+ et 0- sont différents de zéro, le résultat de 1/0+ ou 1/0- existent, 1/0 n'existe pas dans les réels
Il y a continuité entre 0- ; 0 et 0+
Attention, la limite de la fonction n'est pas le produit de la fonction à la limite :
Limite de 1/x en 0+ = l'infini
1/0+ = limite à l'infini
_________________
Ce que je dis n'engage que moi.

Magni- Digressi(f/ve)

- Nombre de messages : 1065
Localisation : 62100
Date d'inscription : 03/05/2016
 Re: Qu'est-ce qu'un segment continu ?
Re: Qu'est-ce qu'un segment continu ?
Ce qui prouve que 0+ et 0- ne sont pas des nombres réels.Magni a écrit:1/0+= limite à l'infini
1/0-= limite à moins l'infini
Si 0+ était un réel, alors 1/0+ serait une simple division entre nombres réels, avec un dénominateur non nul (puisque 0+ n'est pas 0). Et une telle division donne toujours un résultat qui est encore un nombre réel.
Or +infini n'est pas un nombre réel.
Donc l'hypothèse soulignée est fausse : 0+ n'est pas un nombre réel.
Je vois que tu découvres à peine la notion de limite à gauche/droite, qui est pourtant enseignée à l'école secondaire...
Leonhard- Digressi(f/ve)

- Nombre de messages : 194
Date d'inscription : 03/09/2007
 Re: Qu'est-ce qu'un segment continu ?
Re: Qu'est-ce qu'un segment continu ?
Les réels vont jusqu'à la limite à l'infini.
L'infini n'est pas un réel, la limite avant l'infini est dans l'ensemble des réels.
1/0 n'est pas un réel
1/0+ est un réel, ce n'est pas l'infini, c'est la limite avant l'infini.
L'infini n'est pas un réel, la limite avant l'infini est dans l'ensemble des réels.
1/0 n'est pas un réel
1/0+ est un réel, ce n'est pas l'infini, c'est la limite avant l'infini.
_________________
Ce que je dis n'engage que moi.

Magni- Digressi(f/ve)

- Nombre de messages : 1065
Localisation : 62100
Date d'inscription : 03/05/2016
Page 2 sur 5 •  1, 2, 3, 4, 5
1, 2, 3, 4, 5 
Page 2 sur 5
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum

 par Magni Mar 4 Mai 2021 - 10:39
par Magni Mar 4 Mai 2021 - 10:39