Qu'est-ce qu'un segment continu ?

[Leonhard]

Imaginons que l'on ait un ensemble E de nombres entre 0 et 1, ces derniers appartenant aussi à E. Les éléments de cet ensemble occupent donc, chacun, une position sur le segment [0,1].

Énigme 1 :

Supposons que cet ensemble E possède la propriété suivante :

Densité de l'ensemble E :
Entre deux nombres quelconques de E, il y a toujours une infinité d'autres nombres de E.

Question : l'ensemble E est-il nécessairement continu ? Autrement dit, l'ensemble E est-il la totalité du segment [0,1] ?

Énigme 2 :

Supposons que cet ensemble E possède uniquement la propriété suivante :

Indénombrabilité de E :
Les éléments de E sont indénombrables : ils sont en nombre infini et il est impossible de tous les numéroter à l'aide de nombres naturels.

Même question : l'ensemble E est-il nécessairement continu ?



Autrement dit, la continuité est-elle synonyme de densité et/ou d'indénombrabilité ?

Quelle est votre intuition ?

[jean tardieu]

Imaginons que l'on ait un ensemble E de nombres entre 0 et 1,

L'ensemble E est continu puisque tu le poses comme hypothèse. A moins de jouer dans les coins....
C'est comme un mur sans joints.

[Leonhard]

L'ensemble E est continu puisque tu le poses comme hypothèse.

Mais non : on suppose seulement que les points de E sont dans [0,1], mais rien ne dit que tous les points de [0,1] sont dans E.

[quid]

Intuitivement j’aurais dit que si entre deux nombres appartenant à un certain ensemble E, on trouve une infinité de nombres appartenant aussi à E, c’est-à-dire qu’entre deux nombres quelconques de E on trouve toujours au moins un autre nombre E et ceci à l’infini, cela est signe d’un infini continu.

Mais j’ai triché et j’ai regardé un peu sur internet et l’ensemble des nombres rationnels (Q), qui peuvent s’exprimer sous la forme d’une fraction de deux nombres entiers a/b, ont la propriété de densité que tu décris Leonhard. Par exemple entre 1/3001 et 1/3000, que l'on peut noter aussi 2/6002 et 2/6000, on peut insérer 2/6001.

Or on sait aussi qu’entre deux nombres rationnels il y a aussi des nombres non rationnels, des nombres réels (R) qui ne peuvent pas s’exprimer sous la forme d’une fraction et ceci aussi en nombre infini.

Il y a donc des « trous numériques » entre les nombres rationnels et il ne semble donc pas y avoir de continuité.

L’ensemble des nombres rationnels est équipotent aux entiers naturels, c’est-à-dire qu’il existe une bijection (1 pour 1) entre les entiers naturels et les nombres rationnels. Ils sont donc à ce titre, dénombrables. La description d’une bijection pour l’ensemble Q est décrit sur cette page Wiki (https://fr.wikipedia.org/wiki/Ensemble_d%C3%A9nombrable#Les_rationnels). En gros il est possible de construire un arbre qui identifie méthodiquement tous les nombres rationnels. Chaque nœud de l’arbre correspond à un de ces nombres et il y a une infinité de nœuds. Cependant donc, chaque nombre rationnel étant identifié par un nœud, on peut lui associer un nombre entier naturel et inversement en choisissant un nombre naturel, on peut identifier le nœud correspondant dans l’arbre.

Le problème est que si l’on énumère les éléments (nombres) de l’ensemble Q en suivant l’ordre des entiers auxquels ont les a associés, cela ne correspond pas à un ordre numérique du point de vue de la valeur des nombres rationnels correspondants.
Par exemple dans cette bijection (voir page wiki), 5/2 = 2.5 est associé à l’entier 11 et 2/5 = 0.4 est associé à l’entier 12. Cependant 11 est inférieur à 12, mais 2.5 est supérieur à 0.4.

Il y a donc une difficulté. C’est que si l’on conserve l’ordre des valeurs des rationnels et que l’on veut les représenter par un segment de droite à l'aide de points, on ne sera pas capable de le faire. En effet, pour les entiers, entre deux points matérialisant un entier, il n’y a pas d’autre entier à y insérer et une ligne discontinue faite de points (voir problème 2 du fil « l’infini a-t-il une limite » https://digression.forum-actif.net/t1847-l-infini-a-t-il-une-limite#61434) permet bien d’illustrer l'ensemble des entiers. Mais pour les nombres rationnels, il y aura toujours des points à insérer entre chacun et ceci à l’infini.
Du point de vue de l’illustration cela tend plus vers une ligne continue, mais avec des points cependant réputés comme disjoints, ne se touchant pas.

Une question se pose donc. Est-on sûr que l'ensemble des nombres réels rime avec continuité ?
C'est à dire :
1 - On voit une limite de correspondance entre le géométrique et le numérique
2 - Est-on sûr que l'on n'ait pas le même problème qu'avec les nombres rationnels et qu'entre deux nombres réels ne puisse pas s'intercaler une autre classe de nombre. Car en définitive, il me semble que la notation des nombres réels avec leur nombre de chiffres après la virgules qui peut varier à l'infini y est pour beaucoup dans l'intuition que l'on a d'une continuité. Ou autrement dit, si l'on n'accède pas à la continuité à l'aide des nombres rationnels, bien que l'on puisse intercaler à l'infini des nombres de cette classe, alors pourquoi en augmentant le nombre de décimales des nombres réels pour intercaler à l'infini un autre nombre réel entre deux autres accèderait-on plus à la continuité ?

[hks]

Les éléments de cet ensemble occupent donc, chacun, une position sur le segment [0,1].

Pour moi l'idée de position détruit dans l'oeuf l'idée de continuité.

je pars de l'idée suivante : la position et l'identité à soi du nombre sont confondues .
Autrement dit c'est la position ( l'être posé ) qui fait l"identité à soi. Non pas la place (le lieu où) mais le fait d être posé.
A est A identique à lui même si il est posé.

Le Posé et identique à soi (le nombre ou n'importe quel objet posé ) est continu.
(posé par l'intellect ou dans la nature, peu importe)

La discontinuité suppose (ce qui est le cas ) un être posé hors de toute autre position (position d'un autre ou des autres ).
Sinon je dirai que lui et l'autre sont confondus. Confondus en une position.
La discontinuité provient des positions
De ce qu'il soit possible de poser.
Par l'intellect ou dans la nature peu importe ici

Si on se prive de poser
Si aucun individu n'est posé  alors seulement on a une continuité absolue.
.........................
Dans ce que tu dis Leonhard chaque nombre est confondu en une seule position.(ce qui est pensable évidemment)
Mais il y a du fait d être posé une discontinuité, non pas en chaque nombre mais entre eux.
........................
ce qui en revanche est posé  et identique à lui même  (position et identité à soi ) c'est le segment .
En poser un autre  (2 segments) ce serait introduire la discontinuité.

Le segment est  continu en ce qu'il est posé .
mais pas pour le motif qu'il soit composé d'éléments de cet ensemble occupant  chacun, une position
.........................

si tu veux me convaincre il faut montrer une relation entre les nombres  et qui ne soit pas "appartenir à un même ensemble" .
Il me faut un poser dynamique, qui engendre,  qui passe d'une position à l'autre sans rupture.
il me faut une dynamique dans le monde des nombres . Or ton monde des nombre est statique .
C'est toi qui de l'extérieur déplace les pièces du jeu .

[Leonhard]

Intuitivement j’aurais dit que si entre deux nombres appartenant à un certain ensemble E, on trouve une infinité de nombres appartenant aussi à E, c’est-à-dire qu’entre deux nombres quelconques de E on trouve toujours au moins un autre nombre E et ceci à l’infini, cela est signe d’un infini continu.

Mais j’ai triché et j’ai regardé un peu sur internet et l’ensemble des nombres rationnels (Q), qui peuvent s’exprimer sous la forme d’une fraction de deux nombres entiers a/b, ont la propriété de densité que tu décris Leonhard. Par exemple entre 1/3001 et 1/3000, que l'on peut noter aussi 2/6002 et 2/6000, on peut insérer 2/6001.

Or on sait aussi qu’entre deux nombres rationnels il y a aussi des nombres non rationnels, des nombres réels (R) qui ne peuvent pas s’exprimer sous la forme d’une fraction et ceci aussi en nombre infini.

Il y a donc des « trous numériques » entre les nombres rationnels et il ne semble donc pas y avoir de continuité.

Ton intuition initiale était effectivement erronée et tu as donné le bon contre-exemple : l'ensemble des rationnels possède la propriété de densité (entre deux rationnels, il y a toujours une infinité d'autres rationnels), et pourtant cet ensemble n'est pas continu. Donc la densité ne suffit pas pour avoir la continuité.



J'ai mis à jour le message initial pour introduire une seconde énigme.

[jean tardieu]

Mon cher Léonhard, je suis au max de mes capacités cognitives aussi bien avec tes deux énigmes. Mais permets moi, dans le même esprit, de poser à hks une question qui devrait lui plaire : "Ton activité corticale, ou psychique, ou philosophique, est-elle continue ou discontinue dans le courant de ta journée ?"

[jean tardieu]

Bon, je constate que hks n'est pas intéressé. Je ne tiens surtout pas à polluer un sujet aussi passionnant et je fais remarquer que, dès lors que l'on naît et même avant, une activité corticale se met en place, comparable au segment continu, qui est une activité ININTERROMPUE même avec le rêve, laquelle ne s'éteint qu'avec la mort. C'est absolument le point où mathématiques et philosophie peuvent se joindre. (Si on laissait une courbe cérébrale s'étendre tout au long d'une vie, elle ne subirait aucune interruption).

[Leonhard]

On peut encore méditer sur cet aspect contre-intuitif d'un segment comme [0,1] et des nombres réels en général :

Il n'y a pas de point "juste à côté" d'un point donné. (Ce n'est qu'une conséquence de la propriété de densité.)

En même temps, les points du segment [0,1] forment bien, collectivement, une ligne continue, sans "trou" !

Comment un segment peut-il ne pas avoir de "trou" alors que deux points quelconques sont toujours séparés par une distance donnée (dans laquelle se trouve d'autres points) ?!

[Magni]

... Désolé, j'ai perdu l'ancien message qui était ici, j'ai réécrit plus bas une version modifiée.

[Leonhard]

Voici deux segment emboités :  [0,1]∩[1,2]

Ils ne sont pas emboîtés selon le sens du mot "emboîté" dans le théorème des segments emboîtés. Ils seraient emboîtés si l'un des segment est entièrement contenu dans l'autre, ce qui est n'est pas le cas ici. De plus, le théorème ne porte que sur une suite infinie de segments emboîtés, et non sur deux segments.

Difficile de parler de maths quand la simple lecture de l'énoncé d'un théorème fait déjà défaut.

Je ne parle même pas de toutes les confusions mathématiques qui imprègnent tes messages, sur les notions d'adhérence, de limite, de supremum et j'en passe.

[Magni]

Non, deux segments dont l'un est inclus dans l'autre ne donnent un singleton par intersection que lorsque le segment qui est inclus dans l'autre est déjà un singleton.



Et les réels sont un ensemble continu.
Ce n'est pas de ma faute, inutile de s'en prendre à moi.

Les réels sont un ensemble continu et complet, ça signifie qu'il est complet, aucun point de manque.

[Magni]

Lorsque E = ℝ et les fermés sont des intervalles fermés, le théorème prend la forme suivante : soit [an, bn] une suite décroissante de segments de ℝ tels que bn – an tende vers zéro, alors l'intersection des segments [an, bn] est un singleton. Ce corollaire particulier est connu sous le nom de théorème des segments emboîtés.
Fermés emboités

[Magni]

Je ne parle même pas de toutes les confusions mathématiques qui imprègnent tes messages, sur les notions d'adhérence, de limite, de supremum et j'en passe.

Le supremum d'un segment est il oui ou non le dernier point inclus dans un segment ?

Si on exclu ce point du segment, n'y a t il pas toujours un dernier point au segment qui soit le nouveau supremum ?

Le nouveau supremum et l'ancien sont deux singletons !

Dis moi Leonhard, s'il te plais, combien y a t il de réels entre le nouveau supremum et l'ancien ?

[Magni]

J'ai fait un polish de l'esthétique.
Relevez des erreurs si vous en êtes capable. Merci.



Je ne suis pas d'accord avec la prémisse, j'affirme ceci : Dans un segment continu, on ne peut pas toujours trouver une infinité de points entre deux points quelconques.

Entre les points qui sont adjacents, il n'y a pas de points intermédiaires.








[0,1]∩[1,2] = {1} : ces deux segments sont emboités par un singleton qui est emboité entre les deux segments.

Le singleton 1 est emboité dans l'intersection des deux segments.






[0,1[∩[1,2] = {} = Ø : Deux segments non emboités (aucun point n'appartient aux deux, l'intersection est vide, on n'a pas le singleton)
Il n'y a pas de trou entre [0,1[ et [1,2], il n'y a la place pour aucun point supplémentaire entre [0,1[ et [1,2].

Il n'y a qu'un seul point qui est le supremum [0,1[ (et ce point n'est pas 1)
il n'y a qu'un seul point qui est la borne gauche de [1,2] (et ce point est 1).

Le supremum de [0,1[ est un point "adjacent" à la borne inférieur de [1,2], ces deux points se touchent.


Ce qui est adjacent est ce qui se touche. Deux points adjacents se touchent.
Voici la définition :
Adjacent



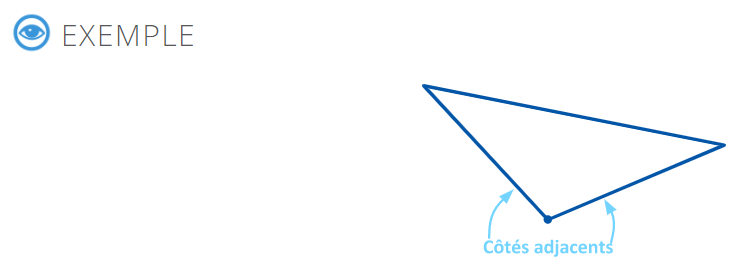
Le triangle est une union des trois cotés et non une addition des trois cotés.

Le sommet entre les deux cotés adjacents ici indiqué appartient aux deux cotés.
Chaque coté a deux sommets.
Deux cotés adjacents ont un seul sommet en commun.

Le sommet est un singleton.
Ce singleton a un et un seul point adjacent sur chacun des deux cotés. Le sommet à deux cotés, il a deux points adjacents.

Sur un tétraèdre, un sommet a trois arêtes adjacentes, il aura trois points adjacents. Les trois points adjacents d'un sommet de tétraèdre ne sont pas adjacents entre eux, il ne se touchent pas car ils ne sont pas sur la même arête (et ils ne sont pas le sommet).

[Leonhard]

Il n'y a qu'un seul point qui est le supremum [0,1[ (et ce point n'est pas 1)

C'est faux. Ce supremum est 1.



Je cite Wikipédia (ici) :

... la borne supérieure (ou le supremum) d'une partie d'un ensemble (partiellement) ordonné est le plus petit de ses majorants.
(...)
l'intervalle ]0, 1[ admet 0 comme borne inférieure et 1 comme borne supérieure

Également la version anglaise (ici) :

Cette formule dit que le supremum de ]0, 1[ et celui de [0, 1] valent tous les deux 1.

Il y a aussi ce document de cours :

Si a et b sont deux réels tels que a < b, sup[a, b[= b.

En l'appliquant à a=0 et b=1, il en découle que tu as tort.

Dans cet autre cours d'analyse universitaire, on trouve :

l'intervalle fermé [a, b] contient sa borne inférieure et sa borne supérieure alors que l’intervalle ouvert ]a, b[ ne contient ni l’une ni l’autre.

Des conclusions analogues valent symétriquement pour la notion d'infimum ou borne inférieure. À la page 8 de ce cours universitaire, on trouve que 0 est l'infimum de ]0, 2] :

0 est bien le plus grand des minorants de A : 0 = inf ]0, 2].

Voici aussi par exemple cette vidéo (à 1'27, on trouve que sup [a, b[ = b) :



Il en découle que tu te trompes ici :

Le supremum de [0,1[ est un point "adjacent" à la borne inférieur de [1,2], ces deux points se touchent.

C'est faux, puisque le supremum de [0, 1[ est 1 lui-même, et non un autre point qui "touche" 1. Il n'y a pas de point qui "touche" 1. Et en même temps, l'intervalle [0, 2] est bel et bien continu en 1.

[Magni]

Il n'y a qu'un seul point qui est le supremum [0,1[ (et ce point n'est pas 1)

C'est faux. Ce supremum est 1.



Je cite Wikipédia (ici) :

... la borne supérieure (ou le supremum) d'une partie d'un ensemble (partiellement) ordonné est le plus petit de ses majorants.
(...)
l'intervalle ]0, 1[ admet 0 comme borne inférieure et 1 comme borne supérieure

Bon d'accord, le supremum peut être en dehors du segment.
Alors comment appelez vous le dernier point qui est dans le segment ? C'est de ça que je parle.





Répondez à cette question s'il vous plait:

Il y a combien de réel entre les points qui sont inclus dans le segment [0,1[ et les points du segment [1,2]


J'affirme : [0,1[∩[1,2] = {} = Ø

Les deux segments se touchent, ils sont adjacents, et ils n'ont aucun point en commun.

Pour qu'ils aient la même borne, il est impératif qu'un point de  [0,1[ touche un point de [1,2], sinon ils ne se touchent pas et ils ne peuvent pas avoir la même borne.

[Magni]

Le dernier point de [0,1[ n'est pas 1, mais il touche 1, car 1 est la borne du segment et la borne touche le segment.

[Leonhard]

Bon d'accord, le supremum peut être en dehors du segment.

Enfin, une avancée !

Alors comment appelez vous le dernier point qui est dans le segment ? C'est de ça que je parle.

Il n'y a pas de dernier point dans le segment [0, 1[. Ce "dernier point", comme tu l'appelles est censé être "le plus grand élément" : il ferait partie de [0, 1[ et serait plus grand que tous les autres. Mais cet élément n'existe pas. Je cite Wikipédia (ici) :

Dans l'ensemble R des nombres réels muni de son ordre usuel, certaines parties majorées n'admettent pas de plus grand élément, par exemple l'intervalle ]0, 1[ des nombres strictement compris entre 0 et 1.

Il y a aussi ce document :

On note qu’une partie majorée (...) de R n'a pas nécessairement de plus grand (...) élément, par exemple, ]0, 1[.

Répondez à cette question s'il vous plait:

Il y a combien de réel entre les points qui sont inclus dans le segment [0,1[ et les points du segment [1,2]


J'affirme : [0,1[∩[1,2] = {} = Ø

Les deux segments se touchent, ils sont adjacents, et ils n'ont aucun point en commun.

D'accord avec cela.

Pour qu'ils aient la même borne, il est impératif qu'un point de  [0,1[ touche un point de [1,2], sinon ils ne se touchent pas et ils ne peuvent pas avoir la même borne.

Cette conviction est intuitive, mais elle est fausse. L'union de [0,1[ et [1,2] est un intervalle continu, et pourtant le nombre 1 n'a pas de "voisin de gauche".

[Magni]

L'union de [0,1[ et [1,2] est un intervalle continu, et pourtant le nombre 1 n'a pas de "voisin de gauche".

Tu veux dire que 1 n'a pas de voisin de gauche dans le segment [1,2] dont il est un élément ?

Ou tu veux dire que 1 n'a pas de voisin de gauche dans la réunion des deux segments [0,2] ?





1/ Si 1 n'a pas de voisin à gauche dans [0,2], alors il n'a pas non plus de voisin à droite, et donc il n'a aucun point adhérent, et il n'y a aucun point qui touche un autre, et les points adhérents n'existent pas, et il n'y a pas de continuité. Donc on n'est pas dans R. Ou alors là il faut m'expliquer, et pas qu'a moi, comment un segment peut être composé seulement de points et être continu s'il est discret entre toutes les paires de points et qu'aucun point ne se touche ?


2/ Si 1 a un voisin a gauche dans [0,2], alors il a aussi un voisin à droite, et donc tous les points adhérent les uns aux autres continument tout le long du segment , il y a continuité donc on est bijectif avec R.







Tu dis qu'on est dans R, mais tu réfutes que des points se touchent.


Est-ce que tu réfutes que R soit un ensemble continu ?
Il y a quoi entre les points hormis l'ensemble vide pour les séparer ?



3/ Si 1 n'a pas de voisin de gauche dans le segment [1,2] dont il est un élément, alors il est la borne unique a gauche.
Question : qu'est qu'il y a entre lui et tous les autres points du segment [1,2] ?

- Rien ?
Et donc s'il n'y a rien entre lui et les autres points, il touche les autres points.

- De la place pour mettre autant de point qu'on veut ?
Alors on n'est dans les dénombrables, non ?

[Magni]

J'affirme : [0,1[∩[1,2] = {} = Ø

Les deux segments se touchent, ils sont adjacents, et ils n'ont aucun point en commun.

D'accord avec cela.

Et cela, je ne le comprends pas du tout !

Es-tu entièrement d'accord avec moi sur ce point ?
Pour moi ce point prouve que des points adjacents existent partout dans les réels !




Si ces deux segments qui n'ont pas de point commun sont adjacents, il faut qu'il y ait au moins un point du segment [0,1[ qui soit adjacent avec au moins un point du segment [1,2]
Non ? Pourquoi pas ? Comment faire autrement ?




Ces deux segments sont adjacents à quel niveau s'il n'ont aucun point adjacent ?

[alain]

Si j' ai bien compris ce que HKS  a voulu dire ... Je suis d' accord avec lui.
C'est bien le " posé " qui détruit la continuité.
Le segment est continu parcequ' il est posé en tant que segment.
Il est continu parce que rien ne vient interrompre sa qualité de segment.
Mais si on le fragmente - et poser les chiffres qu' il contient c' est bien le fragmenter - il devient discontinu et marque en quelque sorte une rupture à chaque chiffre posé.
Si je fais un parallèle avec la conscience ... elle est continue tant qu' aucune idée ne se pose ( ne s' individualise ). C' est ce qui se produit pour la majorité des animaux non humains. 
Elle est discontinue dès qu' une idée se pose ( cela créé une fragmentation ) et c'est cela peut être qui produit la conscience réflexive. Dans notre conscience il y a " retour sur soi " grâce à la discontinuité procédant de l'idée individualisée.
Autrement dit " je " pourrait être une rupture de " suis ", tandis que " je suis" est une continuité.
Ce qui signifie que tout ce qui est statique - ou plutôt pensé comme tel - produit la rupture d' une dynamique et créé une discontinuité.
En ce sens , l' ego est en quelque sorte un point posé sur le segment continu de la conscience.

[Leonhard]

Si ces deux segments qui n'ont pas de point commun sont adjacents, il faut qu'il y ait au moins un point du segment [0,1[ qui soit adjacent avec au moins un point du segment [1,2]
Non ? Pourquoi pas ? Comment faire autrement ?

Non. On peut faire autrement. La clé est que l'on va utiliser une notion d'"adjacence" (en fait, d'adhérence) qui ne va pas lier un point à un autre point, mais un point à un intervalle.

D'abord, il y a la notion de voisinage d'un point : il s'agit d'un intervalle ouvert contenant le point. On peut se représenter un voisinage d'un point par une simple "bulle" autour de ce point.

Ensuite, il y a la notion d'adhérence. Par définition, un point x est adhérent à l'intervalle [0, 1[ si tout voisinage de x intersecte [0, 1[. Il est alors clair que 1 est adhérent à [0, 1[. En ce sens, 1 "colle" à l'intervalle [0, 1[. C'est grâce à cela que l'union de [0, 1[ avec [1, 2] forme l'intervalle continu [0, 2].

Mais l'adhérence n'est pas réciproque : aucun point de [0, 1[ n'est adhérent au singleton {1}. En effet, si x est dans [0, 1[, toute bulle autour de x n'intersecte pas {1} : par exemple, la bulle ]x/2, (x+1)/2[. Autrement dit, aucun point de [0, 1[ ne "colle" directement à 1.



On voit sur l'image que tout bulle autour de 1 intersecte [0, 1[. Par contre, quel que soit le x dans [0, 1[, si on "zoome" suffisamment sur x, on voit qu'il y a toujours moyen de le mettre dans une bulle qui ne contient pas 1. Ceci montre que 1 est adhérent à [0, 1[, mais qu'aucun point de [0, 1[ n'est adhérent à 1.

On a donc les faits suivants :

• 1 "colle" à l'intervalle [0, 1[ pris comme un tout, car toute bulle autour de 1 intersecte cet intervalle.
  
• 1 ne "colle" à aucun point de [0, 1[ en particulier.
  
• Aucun point de [0, 1[ ne "colle" à 1.
  

La continuité spécifique des réels n'apparaît pas si on cherche deux points isolés qui se "toucheraient" directement : cela n'arrive jamais. Elle apparaît, par contre, quand on examine si un point "colle" à un intervalle, et là on trouve ce qu'il faut. En un sens, la continuité est bien une affaire de zones, d'étendues, et non de points isolés.

[Magni]

Si ce que tu dis est juste alors {1} n'a aucun adhérent et les points n'adhèrent qu'aux intervalles et non aux autres points.
Les rationnels adhèrent aux intervalle parce que les rationnels ne se touchent pas entre eux.
Il n'y a pas de dernier rationnel avant {1} parce qu'on peut toujours faire la moyenne rationnelle entre deux rationnels. Aucun rationnel n'est adjacent à un autre rationnel.

Ce n'est pas le cas dans le continu. C'est justement la différence entre le discret et le continu.




Je dis que {1} a une infinité d'adhérents réels, à droite et à gauche sur [0, 2]

Si [0, 1[ n'a pas de dernier point avec la relation d'ordre "usuelle" des réels, c'est parce que la relation "plus petit ou égal" n'ordonne que les nombres qui ont une différence algébriques et il n'y a pas de plus grand nombre algébrique avant 1. Il n'y a pas de différence algébrique entre {1} et ses adhérents. Donc il n'y a pas de dernier réel dans "l'ordre usuel", il y a alors une infinité de point adhérents qui sont "plus petit ou égal" à  {1}.

Mais moi je dis qu'il n'y a qu'un seul point adjacent à {1} qui soit avant {1}. Évidemment ce point adjacent n'est pas un algébrique (et non on ne peut pas mètre un rationnel entre tous les réels car il y a infiniment plus de réels que de rationnels)

Tu confonds nombre algébrique et nombre réel.
Tout ce que tu dis n'est valable que pour les rationnels.





Leonhard, je ne suis pas d'accord avec toi. Inutile de t'en prendre à ma personne.
Répond plutôt à cette question, s'il te plait.


{1} a-t-il oui ou non une infinité de points d'adhérents, à droite et à gauche sur le segment [0, 2] continu ?

[Magni]

On voit sur l'image que tout bulle autour de 1 intersecte [0, 1[. Par contre, quel que soit le x dans [0, 1[, si on "zoome" suffisamment sur x, on voit qu'il y a toujours moyen de le mettre dans une bulle qui ne contient pas 1. Ceci montre que 1 est adhérent à [0, 1[, mais qu'aucun point de [0, 1[ n'est adhérent à 1.

C'est vrai seulement avec des algébriques comme par exemple les rationnels.


Ici tu peux mettre un x' entre x et la borne sans que ce x' ne touche ni x ni la borne, ton x est un rationnel.
x n'adhère pas à 1 parce que tu peux mettre un rationnel entre lui et 1.


Il y a des points adhérents ou il n'y a pas de points adhérents ?
- Il n'y a pas de points adhérent algébriques.
- Il y a une infinité de points adhérents réels pour chaque nombre algébrique, donc tous ces points adhérents à 1 ne sont pas algébriques.



La différence algébrique entre deux points adhérents est nulle.
Mais il existe des réels qui sont différents et qui sont adhérents, les adhérents réels viennent par paquets infini, les adhérents rationnels vienne par paquets d'ensemble vide.

[Contenu sponsorisé]